题目内容
17.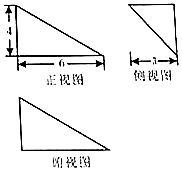 某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )
某几何体的三视图如图.若该几何体的顶点都在球O的表面上,则球O的体积是( )| A. | $\frac{\sqrt{61}}{6}$π | B. | $\frac{\sqrt{61}}{24}$π | C. | $\frac{61\sqrt{61}}{2}$π | D. | $\frac{61\sqrt{61}}{6}$π |
分析 由三视图可知:该几何体为如图所示的三棱锥.其中PA⊥平面ABC,BC⊥平面PAC.设点E为AB的中点,经过点E作OE⊥平面ABC,设点O为三棱锥外接球的球心,作OF⊥AP,垂足为点F.根据OE2+BE2=OF2+PF2,解得OE即可得出.
解答 解:由三视图可知:该几何体为如图所示的三棱锥.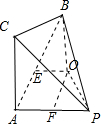 其中PA⊥平面ABC,BC⊥平面PAC.
其中PA⊥平面ABC,BC⊥平面PAC.
设点E为AB的中点,经过点E作OE⊥平面ABC,设点O为三棱锥外接球的球心,
作OF⊥AP,垂足为点F.
则OE2+BE2=OF2+PF2,设OE=x,
则2.52+x2=2.52+(6-x)2,解得x=3.
∴外接球的半径r=$\sqrt{2.{5}^{2}+{3}^{2}}$=$\frac{\sqrt{61}}{2}$.
∴外接球的体积V=$\frac{4π}{3}×(\frac{\sqrt{61}}{2})^{3}$=$\frac{61\sqrt{61}π}{6}$.
故选:D.
点评 本题考查了三棱锥的三视图、球的体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
8.若$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(3,-2),则|2$\overrightarrow{a}$-$\overrightarrow{b}$|=( )
| A. | $\sqrt{17}$ | B. | 1 | C. | $\sqrt{7}$ | D. | $\sqrt{15}$ |
2.某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
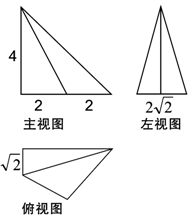

| A. | 136π | B. | 144π | C. | 36π | D. | 34π |
9.已知一个三棱锥的三视图如图所示,则该三棱锥外接球的表面积为( )
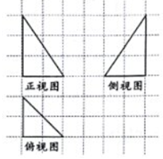

| A. | 17π | B. | 16π | C. | 8π | D. | 20π |
6.-400°的终边在哪个象限( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.已知$\overrightarrow a,\overrightarrow b$均为单位向量,并且它们的夹角为120°,那么$|{\overrightarrow a-2\overrightarrow b}|$等于( )
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | 3 | D. | 7 |
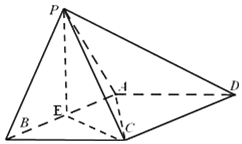 已知四棱锥P-ABCD,底面ABCD为菱形,∠ABC=60°,△PAB是等边三角形,AB=2,PC=$\sqrt{6}$,AB的中点为E
已知四棱锥P-ABCD,底面ABCD为菱形,∠ABC=60°,△PAB是等边三角形,AB=2,PC=$\sqrt{6}$,AB的中点为E