题目内容
11.设定义在R上的函数f(x)的导函数为f′(x),且满足f(2-x)=f(x),$\frac{f′(x)}{x-1}$<0,若x1+x2>2,x1<x2,则( )| A. | f(x1)<f(x2) | B. | f(x1)=f(x2) | ||
| C. | f(x1)>f(x2) | D. | f(x1)与f(x2)的大小不能确定 |
分析 求出函数f(x)的单调性,根据x1+x2>2,x1<x2知f(2-x1)>f(x2),从而求出结论即可.
解答 解:$\frac{f'(x)}{x-1}<0⇒x>1$时,f'(x)<0,即f(x)单减,
由x1+x2>2,x1<x2知:
若x1≥1,则f(x1)>f(x2),
若x1<1,则1<2-x1<x2,
∴f(2-x1)>f(x2),即f(x1)>f(x2),
综上,f(x1)>f(x2),
故选:C.
点评 本题考查了函数的单调性以及导数的应用,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知l是双曲线$C:\frac{x^2}{4}-\frac{y^2}{2}=1$的一条渐近线,P是l上的一点,F1,F2是C的两个焦点,若PF1⊥PF2,则△PF1F2的面积为( )
| A. | 12 | B. | $3\sqrt{2}$ | C. | $\frac{{4\sqrt{2}}}{3}$ | D. | $2\sqrt{3}$ |
6.在平面直角坐标系xOy中,不等式组$\left\{\begin{array}{l}{(x-y-1)(x+y-1)≥0}\\{-1≤x≤3}\end{array}\right.$表示的平面区域的面积为( )
| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
16.心理学家分析发现“喜欢空间想象”与“性别”有关,某数学兴趣小组为了验证此结论,从全球组员中按分层抽样的方法抽取50名同学(男生30人、女生20人),给每位同学立体几何题,代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如表:(单位:人)
(Ⅰ)能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关?
(Ⅱ)经统计得,选择做立体几何题的学生正答率为$\frac{4}{5}$,且答对的学生中男生人数是女生人数的5倍,现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行探究,记抽取的两人中答对的人数为X,求 X的分布列及数学期望.
附表及公式
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 立体几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
(Ⅱ)经统计得,选择做立体几何题的学生正答率为$\frac{4}{5}$,且答对的学生中男生人数是女生人数的5倍,现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行探究,记抽取的两人中答对的人数为X,求 X的分布列及数学期望.
附表及公式
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
20.设偶函数f(x)满足f(x)=2-x-4(x≤0),则{x|f(x-2)>0}=( )
| A. | {x|x<-2或x>4} | B. | {x|x<-2或x>2} | C. | {x|x<0或x>4} | D. | {x|x<0或x>6} |
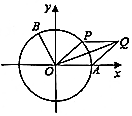 如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$),∠AOB=α.
如图,以坐标原点O为圆心的单位圆与x轴正半轴相交于点A,点B、P在单位圆上,且B(-$\frac{\sqrt{5}}{5}$,$\frac{2\sqrt{5}}{5}$),∠AOB=α.