题目内容

15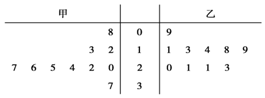．某篮球队甲、乙两名运动员练习罚球，每人练习10组，每组罚球40个．命中个数的茎叶图如图，则下面结论中错误的一个是（　　）
A．乙的众数是21B．甲的中位数是24
C．甲的极差是29D．甲罚球命中率比乙高

分析 利用茎叶图的性质、众数、中位数、极差的定义求解．

解答 解：由茎叶图知，乙的众数是21，故A正确；
甲的中位数是$\frac{22+24}{2}$=23，故B错误；
甲的极差是37-8=29，故C正确；
由茎叶图得到甲的数据集中于茎叶图的左下方，乙的数据集中于茎叶图的右上方，
所以甲罚球命中率比乙高，故D正确．
故选：B．

点评 本题考查命题真假的判断，是基础题，解题时要认真审题，注意茎叶图的性质、众数、中位数、极差的定义的合理运用．

练习册系列答案
相关题目
5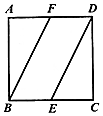．如图，在正方形ABCD中，点E，F分别为边BC，AD的中点，将△ABF沿BF所在直线进行翻折，将△CDE沿DE所在直线进行翻折，在翻折的过程中（　　）
A．点A与点C在某一位置可能重合B．点A与点C的最大距离为$\sqrt{3}$AB
C．直线AB与直线CD可能垂直D．直线AF与直线CE可能垂直
6．在平面直角坐标系xOy中，不等式组$\left\{\begin{array}{l}{（x-y-1）（x+y-1）≥0}\\{-1≤x≤3}\end{array}\right.$表示的平面区域的面积为（　　）
A．4B．8C．12D．16
3．已知θ是第四象限角，且$sin（θ+\frac{π}{4}）=\frac{3}{5}$，则cosθ=$\frac{{7\sqrt{2}}}{10}$．
10．设f（x）=asin 2x+bcos 2x，其中a，b∈R，ab≠0．若f（x）≤|f（$\frac{π}{6}$）|对一切x∈R恒成立，则以下结论正确的是①②④（写出所有正确结论的编号）．
①$f（\frac{5π}{12}）=0$；
②$|{f（\frac{7π}{12}）}$|≥$|{f（\frac{π}{3}）}$|；
③f（x）的单调递增区间是（kπ+$\frac{π}{6}$，kπ+$\frac{2π}{3}$）（k∈Z）；
④f（x）既不是奇函数也不是偶函数．
20．设偶函数f（x）满足f（x）=2-x-4（x≤0），则{x|f（x-2）＞0}=（　　）
A．{x|x＜-2或x＞4}B．{x|x＜-2或x＞2}C．{x|x＜0或x＞4}D．{x|x＜0或x＞6}
7．某车间加工零件的数量x与加工时间y的统计数据如表：
零件数x（个）182022
加工时间y（分钟）273033
现已求得如表数据的回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$中的$\stackrel{∧}{b}$值为0.9，则据此回归模型可以预测，加工100个零件所需要的加工时间约为102分钟．
4．函数f（x）是定义在R上的奇函数，对任意两个不相等的正数x1，x2，都有$\frac{{x}_{2}f（{x}_{1}）-{x}_{1}f（{x}_{2}）}{{x}_{1}-{x}_{2}}$＞0，记a=-log23•f（log${\;}_{\frac{1}{3}}$2），b=f（1），c=4f（0.52），则（　　）
A．c＜b＜aB．b＜a＜cC．c＜a＜bD．a＜b＜c
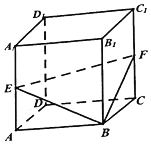5．如图，在棱长为1的正方体ABCD-A1B1C1D1中，点E，F分别是棱AA1，CC1的中点，P是侧面BCC1B1内一点，若A1P∥平面BEF，则线段A1P长度的取值范围是[$\frac{\sqrt{30}}{5}$，$\sqrt{2}$]．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网