题目内容
20.若函数f(x)在其图象上存在不同的两点A(x1,y1),B(x2,y2),其坐标满足条件:|x1x2+y1y2|-$\sqrt{{x_1}^2+y{{{\;}_1}^2}}•\sqrt{{x_2}^2+y{{{\;}_2}^2}}$的最大值为0,则称f(x)为“柯西函数”,则下列函数:
①f(x)=x+$\frac{1}{x}$(x>0);
②f(x)=lnx(0<x<3);
③f(x)=2sinx;
④f(x)=$\sqrt{2{x^2}-8}$.
其中为“柯西函数”的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由柯西不等式得:对任意实数x1,y1,x2,y2,|x1x2+y1y2|-$\sqrt{{x_1}^2+y{{{\;}_1}^2}}•\sqrt{{x_2}^2+y{{{\;}_2}^2}}$≤0恒成立(当且仅当存在实数k,使得x1=kx2,y1=ky2取等号),若函数f(x)在其图象上存在不同的两点A(x1,y1),B(x2,y2),其坐标满足条件:|x1x2+y1y2|-$\sqrt{{x_1}^2+y{{{\;}_1}^2}}•\sqrt{{x_2}^2+y{{{\;}_2}^2}}$的最大值为0,则函数f(x)在其图象上存在不同的两点A(x1,y1),B(x2,y2),使得$\overrightarrow{OA}、\overrightarrow{OB}$共线,即存在点A、B与点O共线,逐一判定即可.
解答 解:由柯西不等式得:对任意实数x1,y1,x2,y2,|x1x2+y1y2|-$\sqrt{{x_1}^2+y{{{\;}_1}^2}}•\sqrt{{x_2}^2+y{{{\;}_2}^2}}$≤0恒成立(当且仅当存在实数k,使得x1=kx2,y1=ky2取等号),若函数f(x)在其图象上存在不同的两点A(x1,y1),B(x2,y2),其坐标满足条件:|x1x2+y1y2|-$\sqrt{{x_1}^2+y{{{\;}_1}^2}}•\sqrt{{x_2}^2+y{{{\;}_2}^2}}$的最大值为0,则函数f(x)在其图象上存在不同的两点A(x1,y1),B(x2,y2),使得$\overrightarrow{OA}、\overrightarrow{OB}$共线,即存在点A、B与点O共线;
对于①,方程kx=x+$\frac{1}{x}$(x>0)不可能有两解,故不存在;
对于②,f(x)=lnx(0<x<3)存在;
对于③,f(x)=2sinx存在;
对于④,f(x)=$\sqrt{2{x^2}-8}$存在.
故选:C.
点评 本题考查了新定义,关键是弄清新定义的含义,属于中档题.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案| A. | (-∞,2] | B. | $[-\frac{5}{2},+∞)$ | C. | $(-∞,-\frac{5}{2})∪(2,+∞)$ | D. | $(-∞,-\frac{5}{2}]∪[2,+∞)$ |
| A. | 2ln2 | B. | 2-ln2 | C. | 7-2ln2 | D. | $\frac{15}{2}$-2ln2 |
| A. | (-3,1) | B. | (-1,3) | C. | (1,+∞) | D. | (-∞,-3) |
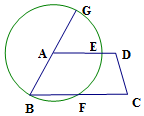 在梯形ABCD中,AD∥BC∠BAD=135°,以A为圆心,AB为半径,作⊙A交AD、BC于E、F两点,并交BA延长线于G点,则$\widehat{BF}$的度数是90°.
在梯形ABCD中,AD∥BC∠BAD=135°,以A为圆心,AB为半径,作⊙A交AD、BC于E、F两点,并交BA延长线于G点,则$\widehat{BF}$的度数是90°.