题目内容
10.已知命题p:函数f(x)=lnx+$\frac{1}{2}{x^2}$-ax为定义域上的增函数,命题q:函数f(x)=x2+$\frac{2}{x}$,$g(x)={(\frac{1}{2})^x}$-a满足对?x1∈[1,2],?x2∈[-1,1]有f(x1)≥g(x2)成立,若命题p∨q为真命题,命题p∧q为假命题,则实数a的取值范围是( )| A. | (-∞,2] | B. | $[-\frac{5}{2},+∞)$ | C. | $(-∞,-\frac{5}{2})∪(2,+∞)$ | D. | $(-∞,-\frac{5}{2}]∪[2,+∞)$ |
分析 命题p真:函数f(x)=lnx+$\frac{1}{2}{x^2}$-ax的导数f′(x)=$\frac{1}{x}+x-a$≥0在(0,+∞)上恒成立,∴a≤($\frac{1}{x}+x$)min;
命题q真:对?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),等价于f(x)min≥g(x)min,于是问题转化为求函数f(x),g(x)的最小值问题.再根据p、q的真假,求出a即可.
解答 解:命题p真:函数f(x)=lnx+$\frac{1}{2}{x^2}$-ax的导数f′(x)=$\frac{1}{x}+x-a$≥0在(0,+∞)上恒成立,
∴a≤($\frac{1}{x}+x$)min,⇒a≤2;
命题q真:当x∈[1,2]时,函数f(x)=x2+$\frac{2}{x}$=x2+$\frac{1}{x}+\frac{1}{x}$≥3$\root{3}{{x}^{2}•\frac{1}{x}•\frac{1}{x}}=3$,所以f(x)min=3;
g(x)=($\frac{1}{2}$)x-a在[-1,1]上单调递减,所以g(x)min=g(1),
对?x1∈[1,2],?x2∈[-1,1]使f(x1)≥g(x2),
等价于f(x)min≥g(x)min,即3≥$\frac{1}{2}-a$,解得a≥-$\frac{5}{2}$
若命题p∨q为真命题,命题p∧q为假命题⇒p、q为一真一假,
当p真,q假时,解得a<-$\frac{5}{2}$,当p假,q真时,解得a>2.
综上:实数a的取值范围是:a<-$\frac{5}{2}$或a>2.
故选:C.
点评 本题考查了利用导数研究函数的单调性,及函数恒成立,转化思想是关键,属于中档题.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
18.设复数z=$\frac{1}{1-i}+{i^7}$,则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 2 |
5.已知抛物线的参数方程为$\left\{\begin{array}{l}x=8{t^2}\\ y=8t\end{array}\right.$(t为参数),则该抛物线的焦点坐标为( )
| A. | (2,0) | B. | (-2,0) | C. | (0,2) | D. | (0,-2) |
2.椭圆3x2+4y2=6的离心率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
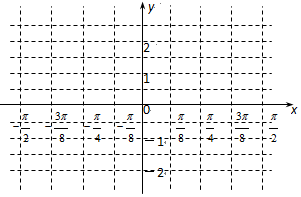 已知函数$f(x)=2cosxsin({x+\frac{π}{3}})-\sqrt{3}{sin^2}x+sinxcosx$.
已知函数$f(x)=2cosxsin({x+\frac{π}{3}})-\sqrt{3}{sin^2}x+sinxcosx$.