Question

3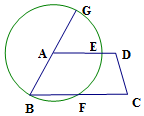．在梯形ABCD中，AD∥BC∠BAD=135°，以A为圆心，AB为半径，作⊙A交AD、BC于E、F两点，并交BA延长线于G点，则$\widehat{BF}$的度数是90°．

Answer 1

分析 连接AF，由平行线的性质得出∠B=45°，由等腰三角形的性质得出∠AFB=∠B=45°，由三角形内角和定理得出∠BAF=90°，即可得出$\widehat{BF}$的度数．

解答 解：连接AF，如图所示：
∵AD∥BC，∠BAD=135°，
∴∠B+∠BAD=180°，
∴∠B=45°，
∵AF=AB，
∴∠AFB=∠B=45°，
∴∠BAF=180°-45°-45°=90°，
∴$\widehat{BF}$的度数为90°．
故答案为90°．

点评 本题考查了梯形的性质、等腰三角形的性质、圆心角、弧、弦的关系；熟练掌握梯形的性质，由等腰三角形的性质求出圆心角的度数是解决问题的关键．