题目内容
长为2的线段AB，其端点在两直角坐标轴上滑动，从原点O做该线段的垂线，求垂足M的轨迹的极坐标，再化为直角坐标方程．
考点：简单曲线的极坐标方程,点的极坐标和直角坐标的互化
专题：坐标系和参数方程
分析：如图所示，可得|OA|=
，|OB|=
．利用|OA|2+|OB|2=22，化为ρ2=4sin2θcos2θ，再利用
即可化为直角坐标方程．
| ρ |
| cosθ |
| ρ |
| sinθ |
|
解答：
解：如图所示，
|OA|=
，|OB|=
．
∴|OA|2+|OB|2=22，
∴
+
=4，
化为ρ2=4sin2θcos2θ，
∴ρ=sin2θ．
化为直角直角方程为（x2+y2）3=4x2y2．
|OA|=
| ρ |
| cosθ |
| ρ |
| sinθ |
∴|OA|2+|OB|2=22，
∴
| ρ2 |
| sin2θ |
| ρ2 |
| cos2θ |
化为ρ2=4sin2θcos2θ，
∴ρ=sin2θ．
化为直角直角方程为（x2+y2）3=4x2y2．
点评：本题考查了把极坐标方程化为直角坐标方程、直角三角形的边角关系，考查了计算能力，属于基础题．
练习册系列答案
相关题目
2011年西安世园会组委会要从五名志愿者中选派四人分别从事翻译、导游、礼仪、司机四项不同的工作，若其中有一名志愿者只能从事司机工作，其余四人均能从事这四项工作，则不同的选派方案共有（ ）
| A、240种 | B、36种 |
| C、24种 | D、48种 |
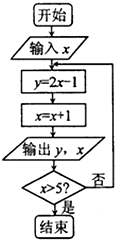如程序框图所示已知集合A={x|框图中输出的x值}，集合B={y|框图中输出的y值}，当x=1时A∩B=（ ）| A、∅ | B、{3} |
| C、{1，3，5} | D、{3，5} |