题目内容
已知在直角坐标系xOy中,曲线C的参数方程为
(θ为参数),在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,直线l的方程为ρsin(θ+
)=0.则曲线C在极坐标系中的方程是 ;直线l被曲线C截得的弦长为 .
|
| π |
| 4 |
考点:参数方程化成普通方程,简单曲线的极坐标方程
专题:坐标系和参数方程
分析:(1)利用sin2θ+cos2θ=1可把曲线C的参数方程化为(x-2)2+y2=4,即x2-4x+y2=0.
(2)直线l的方程为ρsin(θ+
)=0.展开为
(ρsinθ+ρcosθ)=0,可化为x+y=0,再利用点到直线的距离公式、弦长公式即可得出.
(2)直线l的方程为ρsin(θ+
| π |
| 4 |
| ||
| 2 |
解答:
解:(1)曲线C的参数方程为
(θ为参数),利用sin2θ+cos2θ=1可化为(x-2)2+y2=4,即x2-4x+y2=0.
∴曲线C在极坐标系中的方程为ρ2-4ρcosθ=0,
由于ρ=4cosθ包含ρ=0的情况,
∴曲线C在极坐标系中的方程为ρ=4cosθ.
(2)∵直线l的方程为ρsin(θ+
)=0.展开为
(ρsinθ+ρcosθ)=0,可化为x+y=0,
∴圆C的圆心C(2,0)到直线l的距离为d=
,
又∵圆C的半径为r=2,
∴直线l被曲线C截得的弦长l=2
=2
.
|
∴曲线C在极坐标系中的方程为ρ2-4ρcosθ=0,
由于ρ=4cosθ包含ρ=0的情况,
∴曲线C在极坐标系中的方程为ρ=4cosθ.
(2)∵直线l的方程为ρsin(θ+
| π |
| 4 |
| ||
| 2 |
∴圆C的圆心C(2,0)到直线l的距离为d=
| 2 |
又∵圆C的半径为r=2,
∴直线l被曲线C截得的弦长l=2
| r2-d2 |
| 2 |
点评:本题主要考查曲线的参数方程与极坐标方程、直线的极坐标方程、直线与圆相交问题、弦长公式等基础知识,考查运算求解能力以及化归与转化思想,属于基础题.

练习册系列答案
相关题目
下列说法错误的是( )
| A、两两相交且不过同一点的三条直线必在同一平面内 |
| B、过直线外一点有且只有一个平面与已知直线垂直 |
| C、如果共点的三条直线两两垂直,那么它们中每两条直线确定的平面也两两垂直 |
| D、如果两条直线和一个平面所成的角相等,则这两条直线一定平行 |
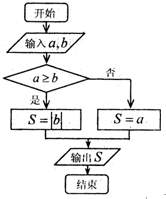
执行如图所示的程序框图,则输出S的值为( )


A、
| ||||
B、
| ||||
C、
| ||||
| D、0 |
 定义某种运算?,a?b的运算原理如图所示:设f(x)=(0?x)x,则f(x)在区间[-2,2]上的最小值为( )
定义某种运算?,a?b的运算原理如图所示:设f(x)=(0?x)x,则f(x)在区间[-2,2]上的最小值为( )| A、-2 | B、-4 | C、2 | D、-8 |
下列命题中是假命题的是( )
| A、?a,b∈R*,lg(a+b)≠lga+lgb |
| B、?φ∈R,使得函数f(x)=sin(2x+φ)是偶函数 |
| C、?α,β∈R,使得cos(α+β)=cosα+cosβ |
| D、?m∈R,使f(x)=(m-1)•x m2-2m+3是幂函数,且在(0,+∞)上递减 |
下列函数既是定义域上的减函数又是奇函数的是( )
| A、f(x)=|x| | ||
B、f(x)=
| ||
| C、f(x)=-x3 | ||
| D、f(x)=x|x| |