��Ŀ����
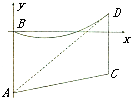 ��һ�α�ֱ��б��AC������������16�ĵ��AB��CD����B��D����һ��10�����ѹ�����ߣ����������BD����������״������BΪԭ�㣬AB����ֱ��ΪY�Ὠ����ͼ��ʾ��ƽ��ֱ������ϵ�����۲ⷢ������ADǡ������������ڵ�D��m��n����
��һ�α�ֱ��б��AC������������16�ĵ��AB��CD����B��D����һ��10�����ѹ�����ߣ����������BD����������״������BΪԭ�㣬AB����ֱ��ΪY�Ὠ����ͼ��ʾ��ƽ��ֱ������ϵ�����۲ⷢ������ADǡ������������ڵ�D��m��n������1����������BD�ķ��̣�
��2�����ݹ����йع涨����ѹ������Χ10����Ϊ����ȫ�����ʵ���һ������1.8���������б�����߶�ʱ�������ѹ�����Ƿ�������˵İ�ȫ������в��
���㣺�����ߵ�Ӧ��
ר�⣺�ۺ���,Բ���ߵĶ��塢�����뷽��
��������1�����������BD�ķ��̣������������ڵ�D�����ߵ�б����AD��б����ȣ���ϵ�D��m��n�����������ϣ�������������BD�ķ��̣�
��2�������ѹ������б��AC�Ĵ�ֱ�������Сֵ�����ɵó����ۣ�
��2�������ѹ������б��AC�Ĵ�ֱ�������Сֵ�����ɵó����ۣ�
���
�⣺��1����������BD�ķ���Ϊy=ax2+bx����
�ߵ�D��m��n����
���������ڵ�D�����ߵ�б��Ϊk=2am+b��
��AD��б��Ϊ
��
��2am+b=
��
��2am2+bm=n+16����
�ߵ�D��m��n�����������ϣ�
��n=am2+bm����
�ɢ٢ڿɵ�a=
��b=
��
�������߷���Ϊy=
x2+
x��
��2��б��AC����ֱ�߷���Ϊy=
x-16��
��ֱ��EF��y���ҷֱ���������AC�ཻ��E��F����
|EF|=��
x2+
x��-��
x-16��=
(x-
)2+12��12��
���ѹ������б��AC�Ĵ�ֱ�������СֵΪ12�ף�����11.8�ף�
�������ѹ���²��������˵İ�ȫ������в��
�ߵ�D��m��n����
���������ڵ�D�����ߵ�б��Ϊk=2am+b��
��AD��б��Ϊ
| n+16 |
| m |
��2am+b=
| n+16 |
| m |
��2am2+bm=n+16����
�ߵ�D��m��n�����������ϣ�
��n=am2+bm����
�ɢ٢ڿɵ�a=
| 16 |
| m2 |
| n-16 |
| m |
�������߷���Ϊy=
| 16 |
| m2 |
| n-16 |
| m |
��2��б��AC����ֱ�߷���Ϊy=
| n |
| m |
��ֱ��EF��y���ҷֱ���������AC�ཻ��E��F����
|EF|=��
| 16 |
| m2 |
| n-16 |
| m |
| n |
| m |
| 16 |
| m2 |
| m |
| 2 |
���ѹ������б��AC�Ĵ�ֱ�������СֵΪ12�ף�����11.8�ף�
�������ѹ���²��������˵İ�ȫ������в��
���������⿼�������ߵ�Ӧ�ã����������ߵ����߷��̣�����ѧ���ļ��������������е��⣮

��ϰ��ϵ�д�
�����Ŀ
�������������������������
�١��ȱ������ε������ڽǾ�Ϊ60�㡱�������⣻
�ڡ���k��0����x2+2x-k=0��ʵ������������⣻
�ۡ�ȫ�������ε������ȡ��ķ����⣮
�١��ȱ������ε������ڽǾ�Ϊ60�㡱�������⣻
�ڡ���k��0����x2+2x-k=0��ʵ������������⣻
�ۡ�ȫ�������ε������ȡ��ķ����⣮
| A��0�� | B��1�� | C��2�� | D��3�� |
����ƽ������£��ú�ֱ��a��b��m��n�������������������ǣ�������
| A����a��m��a��n��m?����n?������a�ͦ� |
| B�������Φ£����ɦ�=a���¡ɦ�=b����a��b |
| C����a��b��b?������a�� |
| D����a?�£�b?�£�a�Φ���b�Φ�����¡Φ��� |