题目内容
已知命题p:任意x∈R,x2+1≥a,命题q:函数f(x)=x2-2ax+1在(-∞,-1]上单调递减.
(1)若命题p为真命题,求实数a的取值范围;
(2)若p和q均为真命题,求实数a的取值范围.
(1)若命题p为真命题,求实数a的取值范围;
(2)若p和q均为真命题,求实数a的取值范围.
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:(1)对于命题p:任意x∈R,x2+1≥a,由x2≥0,即可得到实数a的取值范围;
(2)当q为真命题时,函数f(x)=x2-2ax+1=(x-a)2+1-a2在(-∞,-1]上单调递减.
利用二次函数的单调性可得a≥-1,由于p和q均为真命题,因此
,解得即可.
(2)当q为真命题时,函数f(x)=x2-2ax+1=(x-a)2+1-a2在(-∞,-1]上单调递减.
利用二次函数的单调性可得a≥-1,由于p和q均为真命题,因此
|
解答:
解:(1)对于命题p:任意x∈R,x2+1≥a,∵x2≥0,∴a≤1,即实数a的取值范围是(-∞,1];
(2)当q为真命题时,函数f(x)=x2-2ax+1在(-∞,-1]上单调递减.
∴a≥-1,
∵p和q均为真命题,∴
,解得-1≤a≤1,
∴实数a的取值范围是[-1,1].
(2)当q为真命题时,函数f(x)=x2-2ax+1在(-∞,-1]上单调递减.
∴a≥-1,
∵p和q均为真命题,∴
|
∴实数a的取值范围是[-1,1].
点评:本题考查了二次函数的单调性、简易逻辑的有关知识,属于基础题.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
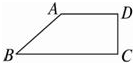 一个水平放置的平面图形的斜二测直观图是直角梯形(如图).∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( )
一个水平放置的平面图形的斜二测直观图是直角梯形(如图).∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( ) A、
| ||||||
B、2+
| ||||||
C、
| ||||||
D、
|
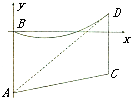 在一段笔直的斜坡AC上竖立两根高16米的电杆AB,CD,过B,D架设一条10万伏高压电缆线.假设电缆线BD呈抛物线形状,现以B为原点,AB所在直线为Y轴建立如图所示的平面直角坐标系,经观测发现视线AD恰与电缆线相切于点D(m,n).
在一段笔直的斜坡AC上竖立两根高16米的电杆AB,CD,过B,D架设一条10万伏高压电缆线.假设电缆线BD呈抛物线形状,现以B为原点,AB所在直线为Y轴建立如图所示的平面直角坐标系,经观测发现视线AD恰与电缆线相切于点D(m,n).