题目内容
对于平面α,β,γ和直线a,b,m,n,下列命题中真命题是( )
| A、若a⊥m,a⊥n,m?α,n?α,则a⊥α |
| B、若α∥β,α∩γ=a,β∩γ=b,则a∥b |
| C、若a∥b,b?α,则a∥α |
| D、若a?β,b?β,a∥α,b∥α,则β∥α. |
考点:命题的真假判断与应用,空间中直线与直线之间的位置关系,空间中直线与平面之间的位置关系,平面与平面之间的位置关系
专题:空间位置关系与距离
分析:A.利用线面垂直的判定定理即可判断出;
B.利用两个平面平行的性质定理即可判断出;
C.利用线面平行的判定定理即可判断出;
D.利用面面平行的判定定理即可得出.
B.利用两个平面平行的性质定理即可判断出;
C.利用线面平行的判定定理即可判断出;
D.利用面面平行的判定定理即可得出.
解答:
解:A.由a⊥m,a⊥n,m?α,n?α,只有当m与n相交时,才能得到a⊥α,因此A不正确;
B.由α∥β,α∩γ=a,β∩γ=b,利用两个平面平行的性质定理即可得出a∥b,因此正确;
C.由a∥b,b?α,则a∥α或a?α;
D.由a?β,b?β,a∥α,b∥α,只有a与b相交时,才能得出β∥α.
故选:B.
B.由α∥β,α∩γ=a,β∩γ=b,利用两个平面平行的性质定理即可得出a∥b,因此正确;
C.由a∥b,b?α,则a∥α或a?α;
D.由a?β,b?β,a∥α,b∥α,只有a与b相交时,才能得出β∥α.
故选:B.
点评:本题综合考查了空间中的线面、面面平行于垂直的位置关系,属于基础题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
变量x,y满足约束条件
,则x+3y最大值是( )
|
| A、2 | B、3 | C、4 | D、5 |
关于x的方程:2x-1+2x2+a=0有两个实数根,则实数a的取值范围可以是( )
A、(
| ||
| B、(1,+∞) | ||
| C、(-∞,1) | ||
D、(-∞,-
|
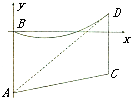 在一段笔直的斜坡AC上竖立两根高16米的电杆AB,CD,过B,D架设一条10万伏高压电缆线.假设电缆线BD呈抛物线形状,现以B为原点,AB所在直线为Y轴建立如图所示的平面直角坐标系,经观测发现视线AD恰与电缆线相切于点D(m,n).
在一段笔直的斜坡AC上竖立两根高16米的电杆AB,CD,过B,D架设一条10万伏高压电缆线.假设电缆线BD呈抛物线形状,现以B为原点,AB所在直线为Y轴建立如图所示的平面直角坐标系,经观测发现视线AD恰与电缆线相切于点D(m,n).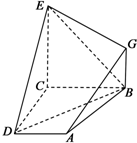 如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=
如图,已知四边形ABCD和BCEG均为直角梯形,AD∥BC,CE∥BG,且∠BCD=∠BCE=