题目内容
下列命题是真命题的有（ ）
①“等边三角形的三个内角均为60°”的逆命题；
②“若k＞0，则方程x2+2x-k=0有实根”的逆否命题；
③“全等三角形的面积相等”的否命题．
①“等边三角形的三个内角均为60°”的逆命题；
②“若k＞0，则方程x2+2x-k=0有实根”的逆否命题；
③“全等三角形的面积相等”的否命题．
| A、0个 | B、1个 | C、2个 | D、3个 |
考点：命题的真假判断与应用
专题：简易逻辑
分析：①利用逆命题的意义即可得出，再利用等边三角形的定义即可得出；
②利用逆否命题的定义即可得出，再利用一元二次方程的是否有实数根与判别式的关系即可得出；
③利用否命题的意义即可得出，进而 判断出真假．
②利用逆否命题的定义即可得出，再利用一元二次方程的是否有实数根与判别式的关系即可得出；
③利用否命题的意义即可得出，进而 判断出真假．
解答：
解：①“等边三角形的三个内角均为60°”的逆命题为“三个内角均为60°的三角形是等边三角形”，正确；
②“若k＞0，则方程x2+2x-k=0有实根”的逆否命题是“方程x2+2x-k=0没有实根，则k≤0”，
对于逆否命题：方程x2+2x-k=0没有实根，则△=4+4k≤0，解得k≤-1，∴k≤0，因此正确；
③“全等三角形的面积相等”的否命题是“不全等的三角形的面积不相等”，不正确．
综上可知：只有①②正确．
故选：C．
②“若k＞0，则方程x2+2x-k=0有实根”的逆否命题是“方程x2+2x-k=0没有实根，则k≤0”，
对于逆否命题：方程x2+2x-k=0没有实根，则△=4+4k≤0，解得k≤-1，∴k≤0，因此正确；
③“全等三角形的面积相等”的否命题是“不全等的三角形的面积不相等”，不正确．
综上可知：只有①②正确．
故选：C．
点评：本题考查了四种命题的定义及其之间的关系，属于基础题．
练习册系列答案
相关题目
设集合An={x|（x-1）（x-n2-4+lnn）＜0}，当n取遍区间（1，3）内的一切实数，所有的集合An的并集是（ ）
| A、（1，13-ln3） |
| B、（1，6） |
| C、（1，+∞） |
| D、（1，2） |
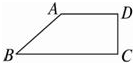一个水平放置的平面图形的斜二测直观图是直角梯形（如图）．∠ABC=45°，AB=AD=1，DC⊥BC，则这个平面图形的面积为（ ） A、
| ||||||
B、2+
| ||||||
C、
| ||||||
D、
|
如图，正方形ABCD的边长为1，延长BA至E，使AE=1，连接EC、ED，则cos2∠CED=（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
在锐角△ABC中，角A，B，C的对边分别为a，b，c．若ccosB+bcosC=2acosA，则角A为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
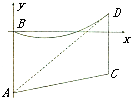在一段笔直的斜坡AC上竖立两根高16米的电杆AB，CD，过B，D架设一条10万伏高压电缆线．假设电缆线BD呈抛物线形状，现以B为原点，AB所在直线为Y轴建立如图所示的平面直角坐标系，经观测发现视线AD恰与电缆线相切于点D（m，n）．