题目内容
已知向量
=(
sinx,sinx),
=(cosx,sinx),函数f(x)=
•
.
(Ⅰ)求函数f(x)的最小正周期及单调递增区间;
(Ⅱ)已知△ABC中,角A,B,C的对边分别为a,b,c,若f(A)=
,a=2,b+c=3,求△ABC的面积.
| m |
| 3 |
| n |
| m |
| n |
(Ⅰ)求函数f(x)的最小正周期及单调递增区间;
(Ⅱ)已知△ABC中,角A,B,C的对边分别为a,b,c,若f(A)=
| 3 |
| 2 |
考点:余弦定理,平面向量数量积的运算,三角函数中的恒等变换应用,正弦定理
专题:三角函数的求值
分析:(Ⅰ)由两向量的坐标,利用平面向量的数量积运算法则列出f(x)解析式,找出ω的值,代入周期公式即可求出函数f(x)的最小正周期,利用正弦函数的单调性即可确定出f(x)单调递增区间;
(Ⅱ)由f(A)=
及第一问的解析式确定出A的度数,再由a,b+c的值,利用余弦定理求出bc的值,利用三角形面积公式即可求出三角形ABC面积.
(Ⅱ)由f(A)=
| 3 |
| 2 |
解答:
解:(Ⅰ)依题意,得f(x)=
•
=
sinxcosx+sin2x=
sin2x+
=sin(2x-
)+
,
∵ω=2,
∴f(x)的最小正周期为π,
由2kπ-
≤2x-
≤2kπ+
,k∈Z,得kπ-
≤x≤kπ+
,k∈Z,
则f(x)的递增区间是[kπ-
,kπ+
],k∈Z;
(Ⅱ)由f(A)=sin(2A-
)+
=
,
∴sin(2A-
)=1,
∵0<A<π,
∴0<2A<2π,即-
<2A-
<
,
∴2A-
=
,即A=
,
∵a=2,b+c=3,
∴根据余弦定理得,4=b2+c2-2bccosA=b2+c2-bc=(b+c)2-3bc=9-3bc,
∴bc=
,
∴S△ABC=
bcsinA=
×
×
=
.
| m |
| n |
| 3 |
| ||
| 2 |
| 1-cos2x |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
∵ω=2,
∴f(x)的最小正周期为π,
由2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
则f(x)的递增区间是[kπ-
| π |
| 6 |
| π |
| 3 |
(Ⅱ)由f(A)=sin(2A-
| π |
| 6 |
| 1 |
| 2 |
| 3 |
| 2 |
∴sin(2A-
| π |
| 6 |
∵0<A<π,
∴0<2A<2π,即-
| π |
| 6 |
| π |
| 6 |
| 11π |
| 6 |
∴2A-
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
∵a=2,b+c=3,
∴根据余弦定理得,4=b2+c2-2bccosA=b2+c2-bc=(b+c)2-3bc=9-3bc,
∴bc=
| 5 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 3 |
| ||
| 2 |
5
| ||
| 12 |
点评:此题考查了余弦定理,平面向量的数量积运算,正弦函数的单调性,三角函数的周期性及其求法,以及三角形面积公式,熟练掌握余弦定理是解本题的关键.

练习册系列答案
相关题目
在锐角△ABC中,角A,B,C的对边分别为a,b,c.若ccosB+bcosC=2acosA,则角A为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
关于x的方程:2x-1+2x2+a=0有两个实数根,则实数a的取值范围可以是( )
A、(
| ||
| B、(1,+∞) | ||
| C、(-∞,1) | ||
D、(-∞,-
|
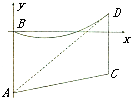 在一段笔直的斜坡AC上竖立两根高16米的电杆AB,CD,过B,D架设一条10万伏高压电缆线.假设电缆线BD呈抛物线形状,现以B为原点,AB所在直线为Y轴建立如图所示的平面直角坐标系,经观测发现视线AD恰与电缆线相切于点D(m,n).
在一段笔直的斜坡AC上竖立两根高16米的电杆AB,CD,过B,D架设一条10万伏高压电缆线.假设电缆线BD呈抛物线形状,现以B为原点,AB所在直线为Y轴建立如图所示的平面直角坐标系,经观测发现视线AD恰与电缆线相切于点D(m,n). 如图是某高中十佳歌手比赛上某一位选手得分的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为
如图是某高中十佳歌手比赛上某一位选手得分的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的方差为