题目内容
已知四棱锥S-ABCD的各棱长为5,底面为正方形,各侧面均为正三角形,求它的表面积.
考点:棱柱、棱锥、棱台的侧面积和表面积
专题:空间位置关系与距离
分析:根据题意,该四棱锥的底面是边长为5的正方形,四个侧面都是边长为5的正三角形,由此结合正方形和正三角形面积计算公式,即可算出该四棱锥的表面积.
解答:
解:作出正四棱锥S-ABCD,如图所示:
 ∵正四棱锥各棱长均为5,
∵正四棱锥各棱长均为5,
∴正四棱锥的底面是边长为5的正方形,一个侧面为边长为5的等边三角形
由此可得侧面△SBC中,面积S=
×52=
因此,它的侧面积为S侧=4×
=25
,
底面积为S底=52=25
∴该正四棱锥的表面积为S=S底=+S侧=25
+25=25(1+
)
 ∵正四棱锥各棱长均为5,
∵正四棱锥各棱长均为5,∴正四棱锥的底面是边长为5的正方形,一个侧面为边长为5的等边三角形
由此可得侧面△SBC中,面积S=
| ||
| 4 |
| 25 |
| 4 |
| 3 |
因此,它的侧面积为S侧=4×
| 25 |
| 4 |
| 3 |
| 3 |
底面积为S底=52=25
∴该正四棱锥的表面积为S=S底=+S侧=25
| 3 |
| 3 |
点评:本题给出所有棱长均为a的正四棱锥,求它的表面积,着重考查了正四棱锥的性质和正方形、正三角形面积计算公式等知识,属于基础题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则cos2∠CED=( )
如图,正方形ABCD的边长为1,延长BA至E,使AE=1,连接EC、ED,则cos2∠CED=( )A、
| ||
B、
| ||
C、
| ||
D、
|
变量x,y满足约束条件
,则x+3y最大值是( )
|
| A、2 | B、3 | C、4 | D、5 |
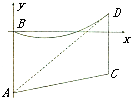 在一段笔直的斜坡AC上竖立两根高16米的电杆AB,CD,过B,D架设一条10万伏高压电缆线.假设电缆线BD呈抛物线形状,现以B为原点,AB所在直线为Y轴建立如图所示的平面直角坐标系,经观测发现视线AD恰与电缆线相切于点D(m,n).
在一段笔直的斜坡AC上竖立两根高16米的电杆AB,CD,过B,D架设一条10万伏高压电缆线.假设电缆线BD呈抛物线形状,现以B为原点,AB所在直线为Y轴建立如图所示的平面直角坐标系,经观测发现视线AD恰与电缆线相切于点D(m,n).