题目内容
12.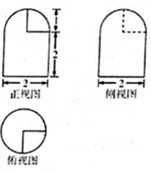 已知一个几何体的三视图如图所示,则该几何体的表面积为( )
已知一个几何体的三视图如图所示,则该几何体的表面积为( )| A. | $\frac{25}{4}$π | B. | 7π | C. | $\frac{29}{4}$π | D. | $\frac{31}{4}$π |
分析 由三视图还原原几何体,原几何体是由一个圆柱和一个半球截去一部分所得,其表面由$\frac{3}{4}$个半球面和3个$\frac{1}{4}$圆及圆柱的侧面和底面组成,分别求解后作和得答案.
解答 由三视图还原原几何体如图,
原几何体是由一个圆柱和一个半球截去一部分所得,
其表面由$\frac{3}{4}$个半球面和3个$\frac{1}{4}$圆及圆柱的侧面和底面组成,它们的面积分别为:
${S}_{\frac{3}{4}半球}=\frac{3}{4}×\frac{1}{2}×4π{r}^{2}=\frac{3}{2}π$;${S}_{截面}=\frac{3}{4}π{r}^{2}=\frac{3}{4}π$;
S圆柱侧面+底面=2πr•2r+πr2=5π.
∴几何体的表面积S=$\frac{3}{2}π+\frac{3}{4}π+5π=\frac{29}{4}π$.
故选:C.
点评 本题考查由三视图求几何体的表面积,关键是由三视图还原原几何体,是中档题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
2.如图是某几何体的三视图,则该几何体的俯视图的周长为( )


| A. | 7$+\sqrt{7}$ | B. | 4+4$\sqrt{3}$ | C. | 4+4$\sqrt{2}$ | D. | 6+2$\sqrt{2}$ |
7.已知函数f(x)是定义在R上的奇函数且单调递增,则不等式f(x)<f(x2)的解集是( )
| A. | (-∞,0)∪(1,+∞) | B. | (-∞,0)∪[1,+∞) | C. | (-∞,0]∪[1,+∞) | D. | (-∞,0)∪(0,1) |
4.长春市的“名师云课”活动自开展以来获得广大家长和学生的高度赞誉,在我市推出的第二季名师云课中,数学学科共计推出36节云课,为了更好地将课程内容呈现给学生,现对某一时段云课的点击量进行统计:
(Ⅰ)现从36节云课中采用分层抽样的方式选出6节,求选出的点击量超过3000的节数.
(Ⅱ)为了更好地搭建云课平台,现将云课进行剪辑,若点击量在区间[0,1000]内,则需要花费40分钟进行剪辑,若点击量在区间(1000,3000]内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中随机取出2节课进行剪辑,求剪辑时间X的分布列与数学期望.
| 点击量 | [0,1000] | (1000,3000] | (3000,+∞) |
| 节数 | 6 | 18 | 12 |
(Ⅱ)为了更好地搭建云课平台,现将云课进行剪辑,若点击量在区间[0,1000]内,则需要花费40分钟进行剪辑,若点击量在区间(1000,3000]内,则需要花费20分钟进行剪辑,点击量超过3000,则不需要剪辑,现从(Ⅰ)中选出的6节课中随机取出2节课进行剪辑,求剪辑时间X的分布列与数学期望.
14.已知在平面直角坐标系xoy中,直线x-ky+2k-1=0与圆x2+y2=4交于A,B两点,若在该圆上还存在一点C,使得$\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}$成立,则实数k的值为( )
| A. | 0 | B. | $\frac{4}{3}$ | C. | 0或$\frac{4}{3}$ | D. | 0或$-\frac{4}{3}$ |
15.要使圆x2+y2+Dx+Ey+F=0与x轴的两个交点分别位于原点的两侧,则有( )
| A. | D2+E2-4F>0,且F<0 | B. | D<0,F>0 | ||
| C. | D≠0,F≠0 | D. | F<0 |