题目内容
7.已知函数f(x)是定义在R上的奇函数且单调递增,则不等式f(x)<f(x2)的解集是( )| A. | (-∞,0)∪(1,+∞) | B. | (-∞,0)∪[1,+∞) | C. | (-∞,0]∪[1,+∞) | D. | (-∞,0)∪(0,1) |
分析 根据题意,由函数的单调性分析可得若f(x)<f(x2),则有x<x2,解可得x的取值范围,即可得答案.
解答 解:根据题意,函数f(x)是定义在R上的奇函数且单调递增,
若f(x)<f(x2),则有x<x2,
解可得x<0或x>1,
即其解集为(-∞,0)∪(1,+∞);
故选:A.
点评 本题考查函数的奇偶性与单调性的综合应用,关键是将不等式f(x)<f(x2)转化为关于x的不等式.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
2.某同学同时投掷两颗骰子,得到点数分别为a,b,则椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e>$\frac{\sqrt{3}}{2}$的概率是( )
| A. | $\frac{1}{18}$ | B. | $\frac{5}{36}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{3}$ |
12.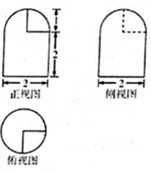 已知一个几何体的三视图如图所示,则该几何体的表面积为( )
已知一个几何体的三视图如图所示,则该几何体的表面积为( )
 已知一个几何体的三视图如图所示,则该几何体的表面积为( )
已知一个几何体的三视图如图所示,则该几何体的表面积为( )| A. | $\frac{25}{4}$π | B. | 7π | C. | $\frac{29}{4}$π | D. | $\frac{31}{4}$π |
19.等比数列{an}中,a2,a6是方程x2-34x+64=0的两根,则a4等于( )
| A. | 8 | B. | -8 | C. | ±8 | D. | 以上都不对 |
9.已知集合A={x|1<x<3},集合B={y|y=x-2,x∈A},则集合A∩B=( )
| A. | {x|1<x<3} | B. | {x|-1<x<3} | C. | {x|-1<x<1} | D. | ∅ |
 如图,在四面体ABCD中,AB=CD=4,AD=BD=5,AC=BC=6,点E,F,G,H分别在棱AD,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是4.
如图,在四面体ABCD中,AB=CD=4,AD=BD=5,AC=BC=6,点E,F,G,H分别在棱AD,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是4.