题目内容
3．已知向量$\overrightarrow a=（1，2），\overrightarrow b=（x，1）$，$\overrightarrow u=\overrightarrow a+2\overrightarrow b\;，\;\overrightarrow v=2\overrightarrow a-\overrightarrow b$，且 $\overrightarrow u$∥$\overrightarrow v$，则实数x的值是$\frac{1}{2}$．分析 利用向量坐标运算性质、向量共线定理即可得出．
解答 解：$\overrightarrow{u}$=（1+2x，4），$\overrightarrow{v}$=（2-x，3），
∵$\overrightarrow u$∥$\overrightarrow v$，∴4（2-x）-3（1+2x）=0，
解得x=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查了向量坐标运算性质、向量共线定理，考查了推理能力与计算能力，属于基础题．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
在某单位的职工食堂中，食堂每天以3元/个的价格从面包店购进面包，然后以5元/个的价格出售．如果当天卖不完，剩下的面包以1元/个的价格卖给饲料加工厂．根据以往统计资料，得到食堂每天面包需求量的频率分布直方图如图所示．食堂某天购进了90个面包，以x（单位：个，60≤x≤110）表示面包的需求量，T（单位：元）表示利润．
14．已知函数$f（x）=\frac{1-x}{{1+{x^2}}}{e^x}$，若f（x1）=f（x2），且x1＜x2，关于下列命题：（1）f（x1）＞f（-x2）；（2）f（x2）＞f（-x1）；（3）f（x1）＞f（-x1）；（4）f（x2）＞f（-x2）．正确的个数为（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
8．已知函数y=f（x）的图象关于x=1对称，且在（1，+∞）上单调递增，设$a=f（\frac{1}{2}）$，b=f（2），c=f（3），则a，b，c的大小关系为（ ）
| A． | b＜a＜c | B． | c＜b＜a | C． | b＜c＜a | D． | a＜b＜c |
如图，在四面体ABCD中，AB=CD=4，AD=BD=5，AC=BC=6，点E，F，G，H分别在棱AD，BD，BC，AC上，若直线AB，CD都平行于平面EFGH，则四边形EFGH面积的最大值是4．
12．
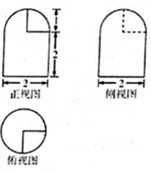已知一个几何体的三视图如图所示，则该几何体的表面积为（ ）
已知一个几何体的三视图如图所示，则该几何体的表面积为（ ）| A． | $\frac{25}{4}$π | B． | 7π | C． | $\frac{29}{4}$π | D． | $\frac{31}{4}$π |