题目内容
20.射手小张在一次射击中射中10环、9环、8环、7环、7环以下的概率分别是0.24、0.28、0.19、0.16、0.13,计算这个射手在一次射击中:(1)射中10环或9环的概率;
(2)至少射中7环的概率.
分析 (1)利用互斥事件概率加法公式能求出这个射手在一次射击中射中10环或9环的概率.
(2)利用对立事件概率计算公式能求出这个射手在一次射击中至少射中7环的概率.
解答 解:(1)∵射手小张在一次射击中射中10环、9环、8环、7环、7环以下的概率分别是0.24、0.28、0.19、0.16、0.13,
∴这个射手在一次射击中射中10环或9环的概率:
p1=0.24+0.28=0.52.
(2)这个射手在一次射击中至少射中7环的概率:p2=1-0.13=0.87.
点评 本题考查概率的求法,考查互斥事件概率加法公式、对立事件概率计算公式等基础知识,考查数据处理能力、运算求解能力,考查函数与方程思想,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.广东佛山某学校参加暑假社会实践活动知识竞赛的学生中,得分在[80,90)中的有16人,得分在[90,100]中的有4人,用分层抽样的方法从得分在[80,100]的学生中抽取一个容量为5的样本,将该样本看成一个整体,从中任意选取2人,则其中恰有1人分数不低于90的概率为( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{2}{5}$ | D. | $\frac{3}{5}$ |
8.已知函数y=f(x)的图象关于x=1对称,且在(1,+∞)上单调递增,设$a=f(\frac{1}{2})$,b=f(2),c=f(3),则a,b,c的大小关系为( )
| A. | b<a<c | B. | c<b<a | C. | b<c<a | D. | a<b<c |
12.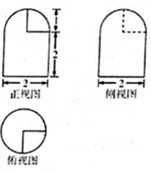 已知一个几何体的三视图如图所示,则该几何体的表面积为( )
已知一个几何体的三视图如图所示,则该几何体的表面积为( )
 已知一个几何体的三视图如图所示,则该几何体的表面积为( )
已知一个几何体的三视图如图所示,则该几何体的表面积为( )| A. | $\frac{25}{4}$π | B. | 7π | C. | $\frac{29}{4}$π | D. | $\frac{31}{4}$π |
2.已知m>0,n>0,则当81m2+n2+$\frac{729}{8mn}$取得最小值时,m-n的值为( )
| A. | -4 | B. | 4 | C. | -8 | D. | 8 |
 如图,在四面体ABCD中,AB=CD=4,AD=BD=5,AC=BC=6,点E,F,G,H分别在棱AD,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是4.
如图,在四面体ABCD中,AB=CD=4,AD=BD=5,AC=BC=6,点E,F,G,H分别在棱AD,BD,BC,AC上,若直线AB,CD都平行于平面EFGH,则四边形EFGH面积的最大值是4.