题目内容
已知矩阵A=
的一个特征值λ=2,其对应的一个特征向量
=
.
(Ⅰ)试求矩阵A-1;
(Ⅱ)求曲线2x-y+1=0经过A-1所对应的变换作用下得到的曲线方程.
|
| a |
|
(Ⅰ)试求矩阵A-1;
(Ⅱ)求曲线2x-y+1=0经过A-1所对应的变换作用下得到的曲线方程.
考点:特征值、特征向量的应用
专题:矩阵和变换
分析:(Ⅰ)直接代入计算;
(Ⅱ)先写出变换,整理即可.
(Ⅱ)先写出变换,整理即可.
解答:
解:(Ⅰ)∵A=
的与特征值λ=2对应的一个特征向量为量
=
,
∴
=2
,
解得
,所以A=
.
∵detA=
=2,
∴A-1=
.
(Ⅱ)矩阵A-1对应的变换为
,
整理,得
…(*)
将(*)代入2x-y+1=0,得2(3x′-y′)-2x′+1=0,
化简,得4x′-2y′+1=0.
故所求的曲线方程为:4x-2y+1=0.
|
| a |
|
∴
|
|
|
解得
|
|
∵detA=
|
∴A-1=
|
(Ⅱ)矩阵A-1对应的变换为
|
整理,得
|
将(*)代入2x-y+1=0,得2(3x′-y′)-2x′+1=0,
化简,得4x′-2y′+1=0.
故所求的曲线方程为:4x-2y+1=0.
点评:本题考查矩阵的计算及变换.

练习册系列答案
相关题目
已知关于x方程x3+ax2+bx+c=0的三个根可以作为一椭圆,一双曲线,一抛物线的离心率,则
的取值范围( )
| b |
| a |
A、(-2,-
| ||
| B、(-2,-1) | ||
C、(-1,-
| ||
D、(-∞,-
|
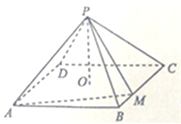 如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,PO=
如图,四棱锥P-ABCD中,底面是以O为中心的菱形,PO⊥底面ABCD,PO=