题目内容
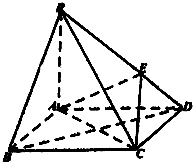 如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=
如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=a,PB=PD=| 2 |
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角B-PA-D的大小;
(Ⅲ)在棱PC上是否存在一点F,使BF∥平面AEC?证明你的结论.
考点:二面角的平面角及求法,直线与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(Ⅰ)证明BD⊥PO,BD⊥AC,利用线面垂直的判定定理证明BD⊥平面PAC;
(Ⅱ)证明∠BAD为二面角B-PA-D的平面角,即可求解;
(Ⅲ)设F为PC中点,取PE中点G,连接FG、BG,设AC、BD交于O,连接OE,由三角形中位线定理可得GF∥EC,OE∥BP,根据面面平行的判定定理可得平面BGF∥平面AEC,由面面平行的性质可得BF∥平面AEC.
(Ⅱ)证明∠BAD为二面角B-PA-D的平面角,即可求解;
(Ⅲ)设F为PC中点,取PE中点G,连接FG、BG,设AC、BD交于O,连接OE,由三角形中位线定理可得GF∥EC,OE∥BP,根据面面平行的判定定理可得平面BGF∥平面AEC,由面面平行的性质可得BF∥平面AEC.
解答:
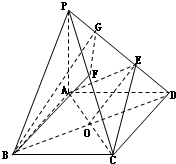 解:设BD∩AC=O,则
解:设BD∩AC=O,则
∵ABCD是菱形,PB=PD,
∴BD⊥PO,BD⊥AC,
∵AC∩PO=O,
∴BD⊥平面PAC;
(Ⅱ)∵PA=AC=a,PB=PD=
a,∠ABC=60°,
∴AB=BC=AC=a,∠PAB=∠PAD=90°,
∴∠BAD为二面角B-PA-D的平面角,
∴二面角B-PA-D的大小为120°;
(Ⅲ)设F为PC中点,取PE中点G,连接FG、BG
设AC、BD交于O,连接OE
由PG=GE,PF=FC得GF∥EC
由DO=OB,DE=EG得OE∥BG
∴平面BGF∥平面AEC
∴BF∥平面AEC
∴F是PC中点时,BF∥平面AEC.
 解:设BD∩AC=O,则
解:设BD∩AC=O,则∵ABCD是菱形,PB=PD,
∴BD⊥PO,BD⊥AC,
∵AC∩PO=O,
∴BD⊥平面PAC;
(Ⅱ)∵PA=AC=a,PB=PD=
| 2 |
∴AB=BC=AC=a,∠PAB=∠PAD=90°,
∴∠BAD为二面角B-PA-D的平面角,
∴二面角B-PA-D的大小为120°;
(Ⅲ)设F为PC中点,取PE中点G,连接FG、BG
设AC、BD交于O,连接OE
由PG=GE,PF=FC得GF∥EC
由DO=OB,DE=EG得OE∥BG
∴平面BGF∥平面AEC
∴BF∥平面AEC
∴F是PC中点时,BF∥平面AEC.
点评:本题考查直线与平面平行的判定,二面角的求法,直线与平面垂直的判定,考查空间想象能力,逻辑思维能力,计算能力,转化思想,是中档题.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
设数列{an}是公差d<0的等差数列,Sn为其前n项和,若S6=5a1+10d,则Sn取最大值时,n=( )
| A、5 | B、6 | C、5或6 | D、6或7 |
已知某个几何体的三视图如右图,根据图中标出的尺寸可得这个几何体的体积是( )
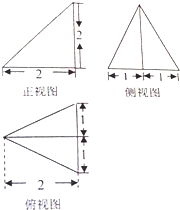

A、
| ||
B、
| ||
C、
| ||
D、
|
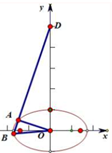 如图,椭圆方程x2+3y2=12,过D(0,10)直线l交椭圆于A、B两点,若OAB为直角三角形,求直线l方程.
如图,椭圆方程x2+3y2=12,过D(0,10)直线l交椭圆于A、B两点,若OAB为直角三角形,求直线l方程.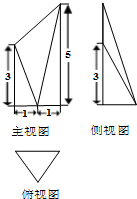 已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为
已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为