题目内容
牛顿冷却模型是指:在常温环境下,如果最初的温度时θ1,环境温度是θ0,则经过时间t(单位:min)后物体的温度θ(单位:℃)将满足;θ=f(t)=θ0+(θ1-θ0)e-kt,其中k为正常数,假设在室内温度为20℃的情况下,一桶咖啡由100℃降低到60℃需要20min.
(1)求f(t)
(2)f′(0)=-2.768的实际意义是什么?
(3)画出函数θ=f(t)在t=20附近的大致图.
(1)求f(t)
(2)f′(0)=-2.768的实际意义是什么?
(3)画出函数θ=f(t)在t=20附近的大致图.
考点:根据实际问题选择函数类型,函数图象的作法
专题:应用题,函数的性质及应用
分析:(1)根据题意,利用公式θ=f(t)=θ0+(θ1-θ0)e-kt,求出k的值;
(2)由f(t)求导数f′(t),用导数的几何意义解释f′(0);
(3)求出t=20时,θ的值,根据函数θ=f(t)的单调性画出大致图形即可.
(2)由f(t)求导数f′(t),用导数的几何意义解释f′(0);
(3)求出t=20时,θ的值,根据函数θ=f(t)的单调性画出大致图形即可.
解答:
解:(1)根据题意,得;
∵θ=f(t)=θ0+(θ1-θ0)e-kt,其中k为正常数,
当θ0=20,θ1=100,θ=60,t=20时,
20+(100-20)•e-20k=60,
即e-20k=
,
解得k=
,
∴f(t)=20+80e-
t;
(2)∵f(t)=20+80e-
t,
∴f′(t)=80•(-
)•e-
t
=-4ln2•e-
t,
∴f′(0)=-4ln2≈-2.768,
它表示温度降低到0C°的变化率;
(3)∵θ=f(t)=20+80e-
t,
∴当t=20时,θ=f(20)=20+80e-ln2=20+80×2-1=60,
∴画出函数θ=f(t)在t=20附近的大致图形,如图所示.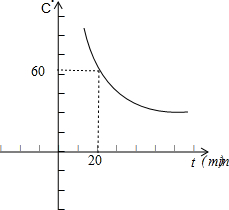
∵θ=f(t)=θ0+(θ1-θ0)e-kt,其中k为正常数,
当θ0=20,θ1=100,θ=60,t=20时,
20+(100-20)•e-20k=60,
即e-20k=
| 1 |
| 2 |
解得k=
| ln2 |
| 20 |
∴f(t)=20+80e-
| ln2 |
| 20 |
(2)∵f(t)=20+80e-
| ln2 |
| 20 |
∴f′(t)=80•(-
| ln2 |
| 20 |
| ln2 |
| 20 |
=-4ln2•e-
| ln2 |
| 20 |
∴f′(0)=-4ln2≈-2.768,
它表示温度降低到0C°的变化率;
(3)∵θ=f(t)=20+80e-
| ln2 |
| 20 |
∴当t=20时,θ=f(20)=20+80e-ln2=20+80×2-1=60,
∴画出函数θ=f(t)在t=20附近的大致图形,如图所示.

点评:本题考查了函数模型的应用问题,也考查了函数的图象与性质的应用问题,导数的几何意义的应用问题,是综合性题目.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
已知在△ABC中,D是AB边上的一点,
=λ(
+
),|
|=2,|
|=1,若
=
,
=
,则用
,
表示
为( )
| CD |
| ||
|
|
| ||
|
|
| CA |
| CB |
| CA |
| b |
| CB |
| a |
| a |
| b |
| CD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
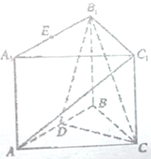 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,D是AB的中点.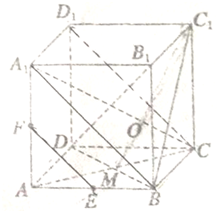 如图,在正方体ABCD-A1B1C1D1,对角线A1C与平面BDC1交于点O.AC、BD交于点M、E为AB的中点,F为AA1的中点,
如图,在正方体ABCD-A1B1C1D1,对角线A1C与平面BDC1交于点O.AC、BD交于点M、E为AB的中点,F为AA1的中点,