题目内容
在△ABC中,已知a=4,b=2
-2,B=15°,求A、C及c的值.
| 3 |
考点:正弦定理,余弦定理
专题:解三角形
分析:由sin15°=sin(45°-30°)=
,由正弦定理可得:
=
=
,sinA=
,又a>b,A∈(0,π),可得A=45°或135°,即可得到C.
| ||||
| 4 |
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| ||
| 2 |
解答:
解:∵sin15°=sin(45°-30°)=sin45°cos30°-cos45°sin30°=
,
由正弦定理可得:
=
=
,
∴sinA=
=
=
,
又a>b,A∈(0,π),
∴A=45°或135°,
∴C=120°或30°.
∴c=
=2
或2
.
| ||||
| 4 |
由正弦定理可得:
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴sinA=
| asinB |
| b |
| 4sin15° | ||
2
|
| ||
| 2 |
又a>b,A∈(0,π),
∴A=45°或135°,
∴C=120°或30°.
∴c=
| asinC |
| sinA |
| 6 |
| 2 |
点评:本题考查了两角和差的正弦公式、正弦定理、三角形内角和定理、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知实数x,y满足
,则z=(
)x•(
)y的最小值为( )
|
| 1 |
| 9 |
| 1 |
| 3 |
A、
| ||
| B、1 | ||
C、
| ||
D、
|
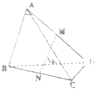 如图,在四面体ABCD中,若M、N分别是棱AD、BC的中点,AC=BD=6,MN=3
如图,在四面体ABCD中,若M、N分别是棱AD、BC的中点,AC=BD=6,MN=3 设α∈(0,π),且α≠
设α∈(0,π),且α≠