题目内容
已知数列{an}的首项a1=1,an+1=3Sn(n∈N*),则下列结论正确的是( )
| A、数列是{an}等比数列 |
| B、数列a2,a3,…,an是等比数列 |
| C、数列是{an}等差数列 |
| D、数列a2,a3,…,an是等差数列 |
考点:等比关系的确定
专题:等差数列与等比数列
分析:在数列递推式中取n=n-1得另一递推式,作差后得到an+1=4an(n≥2),由已知求得a2=3,说明数列从第二项起是公比为4的等比数列.
解答:
解:由an+1=3Sn(n≥1),得
an=3Sn-1(n≥2),
两式作差得:an+1-an=3an(n≥2),
即an+1=4an(n≥2),
∵a1=1,an+1=3Sn(n≥1),
∴a2=3.
∴数列a2,a3,…,an是公比为4的等比数列.
故选:B.
an=3Sn-1(n≥2),
两式作差得:an+1-an=3an(n≥2),
即an+1=4an(n≥2),
∵a1=1,an+1=3Sn(n≥1),
∴a2=3.
∴数列a2,a3,…,an是公比为4的等比数列.
故选:B.
点评:本题考查了数列递推式,考查了等比关系的确定,是基础题.

练习册系列答案
相关题目
在△ABC中,已知∠BAC=150°,且
•
=-4
,设D是△ABC内部的一点,△DAB、△DBC、△DCA的面积依次为m、n、p,则当p=1时,
+
的最小值为( )
| AB |
| AC |
| 3 |
| 1 |
| m |
| 4 |
| n |
| A、3 | B、5 | C、7 | D、9 |
已知函数f(x)=x2+mx-2n,m,n∈[0,2],则使f(1)≤0成立的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知点P(x,y)的坐标满足条件
,那么点P到直线3x-4y-13=0的最小值为( )
|
A、
| ||
| B、2 | ||
C、
| ||
| D、1 |
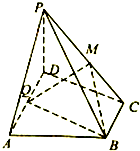 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD||BC,PD⊥底面ABCD,
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD||BC,PD⊥底面ABCD,
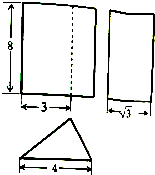 设某几何体的三视图如图所示(尺寸的长度单位为:m),若该几何体的各个顶点都在同一球面上,则此球面的表面积等于
设某几何体的三视图如图所示(尺寸的长度单位为:m),若该几何体的各个顶点都在同一球面上,则此球面的表面积等于