题目内容
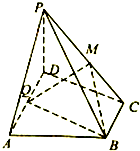 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD||BC,PD⊥底面ABCD,∠ADC=90°,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD||BC,PD⊥底面ABCD,∠ADC=90°,BC=| 1 |
| 2 |
(Ⅰ)试确定点M的位置,使得PA||平面BMQ,并证明你的结论;
(Ⅱ)若PM=2MC,求二面角P-BQ-M的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)当M为PC中点时,PA∥平面BMQ,连结AC交BQ于N,连结MN,则MN∥PA,由此能证明PA∥平面BMQ.
(Ⅱ)以点D为原点DA,DC,DP所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角P-BQ-M的余弦值.
(Ⅱ)以点D为原点DA,DC,DP所在直线分别为x,y,z轴,建立空间直角坐标系,利用向量法能求出二面角P-BQ-M的余弦值.
解答:
 解:(Ⅰ)当M为PC中点时,PA∥平面BMQ,…(2分)
解:(Ⅰ)当M为PC中点时,PA∥平面BMQ,…(2分)
理由如下:连结AC交BQ于N,连结MN,
因为∠ADC=90°,Q为AD的中点,
所以N为AC的中点.
当M为PC的中点,即PM=MC时,MN为△PAC的中位线,…(4分)
故MN∥PA,又MN?平面BMQ,PA?平面BMQ,
所以PA∥平面BMQ.…(5分)
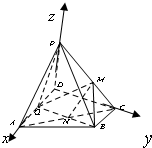
(Ⅱ)由题意,以点D为原点DA,DC,DP所在直线分别为x,y,z轴,
建立空间直角坐标系,…(6分)
则P(0,0,2),Q(1,0,0),B(1,2,0),…(7分)
由PM=2MC可得点M(0,
,
),
所以
=(1,0-2),
=(0,2,0),
=(-1,
,
),
设平面PQB的法向量为
=(x,y,z),
则
令z=1,∴
=(2,0,1),…(9分)
同理平面MBQ的法向量为
=(
,0,1),…(10分)
设二面角大小为θ,cosθ=
=
.
∴二面角P-BQ-M的余弦值为
.…(12分)
 解:(Ⅰ)当M为PC中点时,PA∥平面BMQ,…(2分)
解:(Ⅰ)当M为PC中点时,PA∥平面BMQ,…(2分)理由如下:连结AC交BQ于N,连结MN,
因为∠ADC=90°,Q为AD的中点,
所以N为AC的中点.
当M为PC的中点,即PM=MC时,MN为△PAC的中位线,…(4分)
故MN∥PA,又MN?平面BMQ,PA?平面BMQ,
所以PA∥平面BMQ.…(5分)
(Ⅱ)由题意,以点D为原点DA,DC,DP所在直线分别为x,y,z轴,
建立空间直角坐标系,…(6分)
则P(0,0,2),Q(1,0,0),B(1,2,0),…(7分)
由PM=2MC可得点M(0,
| 4 |
| 3 |
| 2 |
| 3 |
所以
| PQ |
| QB |
| QM |
| 4 |
| 3 |
| 2 |
| 3 |
设平面PQB的法向量为
| n1 |
则
|
令z=1,∴
| n1 |
同理平面MBQ的法向量为
| n2 |
| 2 |
| 3 |
设二面角大小为θ,cosθ=
| ||||
|
|
7
| ||
| 65 |
∴二面角P-BQ-M的余弦值为
7
| ||
| 65 |
点评:本题考查使得直线与平面平行的点的位置确定,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
设f(x)=
+2x,0<a<b<e,则( )
| lnx |
| x |
| A、f(a)>f(b) |
| B、f(a)<f(b) |
| C、f(a)=f(b) |
| D、f(a)f(b)>0 |
已知数列{an}的首项a1=1,an+1=3Sn(n∈N*),则下列结论正确的是( )
| A、数列是{an}等比数列 |
| B、数列a2,a3,…,an是等比数列 |
| C、数列是{an}等差数列 |
| D、数列a2,a3,…,an是等差数列 |
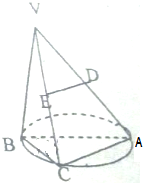 如图,AB是圆O的直径,AB=2,点C在圆O上,且∠ABC=60°,V到圆O所在的平面的距离为3,且VC垂直于圆O所在的平面,D,E分别是VA,VC的中点.
如图,AB是圆O的直径,AB=2,点C在圆O上,且∠ABC=60°,V到圆O所在的平面的距离为3,且VC垂直于圆O所在的平面,D,E分别是VA,VC的中点.