题目内容
某班有班干部6人,其中有女同学4人,所有班干部中只有男同学甲和女同学乙参加过社区服务,今抽调3名班干部组成青年志愿者活动小组到社区服务,小组中必须有男有女,且甲、乙两人至少有一人参加,那么不同的选派方法共有 种.
考点:计数原理的应用
专题:应用题,排列组合
分析:求出抽调3名班干部组成青年志愿者活动小组到社区服务,小组中必须有男有女的所有情况,减去甲、乙两人都不参加的情况,即可得出结论.
解答:
解:抽调3名班干部组成青年志愿者活动小组到社区服务,小组中必须有男有女,共有
-
=16种,
甲、乙两人都不参加,共有
-
=3,
所以甲、乙两人至少有一人参加,那么不同的选派方法共有13种.
故答案为:13.
| C | 3 6 |
| C | 3 4 |
甲、乙两人都不参加,共有
| C | 3 4 |
| C | 3 3 |
所以甲、乙两人至少有一人参加,那么不同的选派方法共有13种.
故答案为:13.
点评:本题考查组合知识,考查小时利用数学知识解决实际问题的能力,属于中档题.

练习册系列答案
相关题目
复数
(i是虚数单位)化简的结果是( )
| 1-i |
| 1+i |
| A、1 | B、-1 | C、i | D、-i |
复数(
)2(i是虚数单位)化简的结果是( )
| 1-i |
| 1+i |
| A、1 | B、-1 | C、i | D、-i |
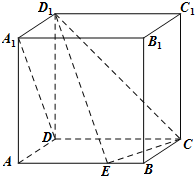 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点.
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E是棱AB上的动点. 已知正三棱柱ABC-A1B1C的底面边长为4cm,高为7cm,则当一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的路程最短时,质点沿着侧面的前进方向所在直线与底面ABC所成角的余弦值为
已知正三棱柱ABC-A1B1C的底面边长为4cm,高为7cm,则当一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的路程最短时,质点沿着侧面的前进方向所在直线与底面ABC所成角的余弦值为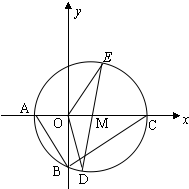 如图,△ABC中,
如图,△ABC中,