题目内容
已知等差数列{an}的前n项和为Sn,且满足S4=12,S6=30.
(Ⅰ)求an;
(Ⅱ)设数列{bn}满足bn+1=2bn-an且b1=4,
(i)证明:数列{bn-2n}是等比数列,并求{bn}的通项;
(ii)当n≥2时,比较bn-1•bn+1与bn2的大小.
(Ⅰ)求an;
(Ⅱ)设数列{bn}满足bn+1=2bn-an且b1=4,
(i)证明:数列{bn-2n}是等比数列,并求{bn}的通项;
(ii)当n≥2时,比较bn-1•bn+1与bn2的大小.
考点:数列的求和,等差数列的性质
专题:综合题,等差数列与等比数列
分析:(Ⅰ)设等差数列{an}的公差为d,依题意,布列关于首项a1与公差d的方程组,解之即可求得an;
(Ⅱ)(i)由已知得bn+1=2bn-2n+2,易证数列{bn-2n}是以2为首项,2为公比的等比数列,继而可得{bn}的通项;
(ii)作差比较,整理可得bn-1•bn+1-bn2=2n(n-3)-4,通过对n取值情况的讨论,可得bn-1•bn+1与bn2的大小.
(Ⅱ)(i)由已知得bn+1=2bn-2n+2,易证数列{bn-2n}是以2为首项,2为公比的等比数列,继而可得{bn}的通项;
(ii)作差比较,整理可得bn-1•bn+1-bn2=2n(n-3)-4,通过对n取值情况的讨论,可得bn-1•bn+1与bn2的大小.
解答:
解:(Ⅰ)设等差数列{an}的公差为d,由已知得
,…3分
解得
,所以an=2n-2…5分
(Ⅱ)(i)由已知得bn+1=2bn-2n+2,即bn+1-2(n+1)=2(bn-2n)且b1-2=2,
所以数列{bn-2n}是以2为首项,2为公比的等比数列…8分
则bn-2n=2n,所以bn=2n+2n…10分
(ii)当n≥2时,bn-1•bn+1-bn2=[2n-1+2(n-1)][2n+1+2(n+1)]-(2n+2n)2
=22n+2n(n+1)+2n×4(n-1)+4(n2-1)-(22n+4n×2n+4n2)
=2n(n-3)-4…13分
所以当n=2或n=3时,bn-1•bn+1<bn2…14分
当n≥4时,bn-1•bn+1>bn2…15分
|
解得
|
(Ⅱ)(i)由已知得bn+1=2bn-2n+2,即bn+1-2(n+1)=2(bn-2n)且b1-2=2,
所以数列{bn-2n}是以2为首项,2为公比的等比数列…8分
则bn-2n=2n,所以bn=2n+2n…10分
(ii)当n≥2时,bn-1•bn+1-bn2=[2n-1+2(n-1)][2n+1+2(n+1)]-(2n+2n)2
=22n+2n(n+1)+2n×4(n-1)+4(n2-1)-(22n+4n×2n+4n2)
=2n(n-3)-4…13分
所以当n=2或n=3时,bn-1•bn+1<bn2…14分
当n≥4时,bn-1•bn+1>bn2…15分
点评:本题考查数列的求和,着重考查等差数列的通项公式与等比关系的确定,突出考查作差法在比较大小中的应用,属于难题.

练习册系列答案
相关题目
函数f(x)的图象如图所示,则不等式(x+3)•f′(x)<0的解集为( )
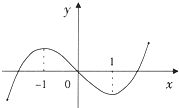

| A、(-∞,-3)∪(-1,1) |
| B、(-∞,-3) |
| C、(-∞,-1)∪(1,+∞) |
| D、(1,+∞) |