题目内容
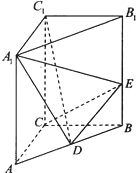
已知四棱锥P-ABCD的侧棱长与底面边长都相等,点E是PB的中点,则异面直线AE与PD所成角的余弦值为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:异面直线及其所成的角
专题:空间角
分析:设棱长都为1,连接AC,BD交于点O,连接OE.由于所有棱长都相等,不妨设ABCD是正方形.利用三角形的中位线定理可得:OE∥PD,因此∠AEO或其补角为异面直线AE与PD所成的角.在△OAE中,由余弦定理得cos∠AEO=
.
| AE2+OE2-OA2 |
| 2AE•OE |
解答:
解:设棱长都为1,连接AC,BD交于点O,连接OE.
∵所有棱长都相等,不妨设ABCD是正方形.
∴ O是BD的中点,且OE∥PD,
O是BD的中点,且OE∥PD,
∴∠AEO或其补角为异面直线AE与PD所成的角.
又OE=
PD=
,AE=
AB=
,OA=
AC=
=
.
在△OAE中,由余弦定理得cos∠AEO=
=
.
∵所有棱长都相等,不妨设ABCD是正方形.
∴
 O是BD的中点,且OE∥PD,
O是BD的中点,且OE∥PD,∴∠AEO或其补角为异面直线AE与PD所成的角.
又OE=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 12+12 |
| ||
| 2 |
在△OAE中,由余弦定理得cos∠AEO=
| AE2+OE2-OA2 |
| 2AE•OE |
| ||
| 3 |
点评:本题考查了异面直线所成的角、三角形的中位线定理、余弦定理、正方形的性质等基础知识与基本技能方法,考查了推理能力,属于基础题

练习册系列答案
相关题目
函数y=
的单调递减区间是( )
| lnx |
| x |
| A、(e-1,+∞) |
| B、(0,e-1) |
| C、(-∞,e-1) |
| D、(e,+∞) |
函数f(x)=
-6+2x的零点一定位于区间( )
| 1 |
| x |
| A、(3,4) |
| B、(2,3) |
| C、(1,2) |
| D、(5,6) |
函数f(x)的图象如图所示,则不等式(x+3)•f′(x)<0的解集为( )
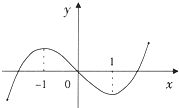

| A、(-∞,-3)∪(-1,1) |
| B、(-∞,-3) |
| C、(-∞,-1)∪(1,+∞) |
| D、(1,+∞) |
函数f(x)=x3+3x2+3x的单调增区间为( )
| A、(-∞,+∞) |
| B、(-∞,-1) |
| C、(0,+∞) |
| D、(-1,+∞) |