题目内容
已知直线y=kx+1与双曲线x2-y2=1的左支相交于不同的两点A,B,线段AB的中点为点M,定点C(-2,0).
(1)求实数k的取值范围;
(2)求直线MC在y轴上的截距的取值范围.
(1)求实数k的取值范围;
(2)求直线MC在y轴上的截距的取值范围.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由直线y=kx+1代入双曲线x2-y2=1,可得(1-k2)x2+2kx-2=0,再直线y=kx+1与双曲线x2-y2=1的左支相交于不同的两点A,B,利用根的判别式和韦达定理能求出k的取值范围.
(2)由直线l经过C(-2,0)及线段AB的中点M,知直线MC的方程为x-(-2k2+k+2)y+2=0,令x=0,解得直线l在y轴上的截距b=
.设f(k)=-2k2+k+2=-2(k-
)2+
,则f(k)在(1,
)上是减函数,由此能求出直线l在y轴上的截距b的取值范围.
(2)由直线l经过C(-2,0)及线段AB的中点M,知直线MC的方程为x-(-2k2+k+2)y+2=0,令x=0,解得直线l在y轴上的截距b=
| 2 |
| -2k2+k+2 |
| 1 |
| 4 |
| 17 |
| 8 |
| 2 |
解答:
解:(1)直线y=kx+1代入双曲线x2-y2=1,可得(1-k2)x2-2kx-2=0,
∵直线y=kx+1与双曲线x2-y2=1的左支相交于不同的两点A,B,
∴1-k2≠0,△=4k2+8(1-k2)>0,
<0,
>0
∴解得1<k<
.
∴k的取值范围是(1,
).
(2)设M(x0,y0),∴x0=
,y0=kx0+1=
,
∵直线l经过C(-2,0)及线段AB的中点M,
∴直线MC的方程为:
=
,整理,得x-(-2k2+k+2)y+2=0,
令x=0,解得直线l在y轴上的截距b=
.
设f(k)=-2k2+k+2=-2(k-
)2+
,
则f(k)在(1,
)上是减函数,
∴f(
)<f(k)<f(1),且f(k)≠0,
∴-2+
<f(k)<1,且f(k)≠0,
∴b<-2-
,或b>2,
故直线l在y轴上的截距b的取值范围是(-∞,-2-
)∪(2,+∞).
∵直线y=kx+1与双曲线x2-y2=1的左支相交于不同的两点A,B,
∴1-k2≠0,△=4k2+8(1-k2)>0,
| 2k |
| 1-k2 |
| -2 |
| 1-k2 |
∴解得1<k<
| 2 |
∴k的取值范围是(1,
| 2 |
(2)设M(x0,y0),∴x0=
| k |
| 1-k2 |
| 1 |
| 1-k2 |
∵直线l经过C(-2,0)及线段AB的中点M,
∴直线MC的方程为:
| y | ||
|
| x+2 | ||
|
令x=0,解得直线l在y轴上的截距b=
| 2 |
| -2k2+k+2 |
设f(k)=-2k2+k+2=-2(k-
| 1 |
| 4 |
| 17 |
| 8 |
则f(k)在(1,
| 2 |
∴f(
| 2 |
∴-2+
| 2 |
∴b<-2-
| 2 |
故直线l在y轴上的截距b的取值范围是(-∞,-2-
| 2 |
点评:本题考查直线的斜率的取值范围的求法,考查直线纵截距的取值范围的求法,考查学生分析解决问题的能力,属于中档题..

练习册系列答案
相关题目
下列函数中周期为π且图象关于直线x=
对称的函数是( )
| π |
| 3 |
A、y=2sin(
| ||||
B、y=2sin(2x-
| ||||
C、y=2sin(2x+
| ||||
D、y=2sin(
|
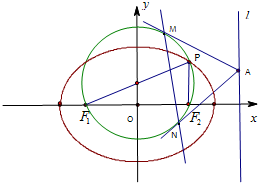 已知椭圆
已知椭圆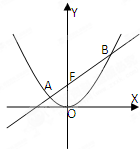 抛物线C:x2=2py(p>0)的焦点为F,O为坐标原点;当抛物线上点N的纵坐标为1时,|NF|=2,已知直线l经过抛物线C的焦点F,且与抛物线C交于A,B两点
抛物线C:x2=2py(p>0)的焦点为F,O为坐标原点;当抛物线上点N的纵坐标为1时,|NF|=2,已知直线l经过抛物线C的焦点F,且与抛物线C交于A,B两点 若F1、F2分别是椭圆
若F1、F2分别是椭圆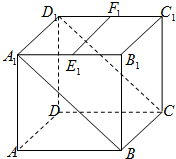 如图,A1B1C1D-ABCD为边长为a的正方体,E,F分别是A1B1,C1D的中点,过EF作正方体截面,若截面平行于平面A1BCD1,则截面的面积为
如图,A1B1C1D-ABCD为边长为a的正方体,E,F分别是A1B1,C1D的中点,过EF作正方体截面,若截面平行于平面A1BCD1,则截面的面积为