题目内容

若方程x2+2x+m=0有实根，-mx2+2x+1=0无实根，则m∈
 
．
考点：二次函数的性质
专题：函数的性质及应用
分析：当m=0时，两个方程均有根，不满足要求，当m≠0时，若二次方程x2+2x+m=0有实根，-mx2+2x+1=0无实根，可得
4-4m≥0
4+4m＜0
，解得m的范围
解答： 解：当m=0时，两个方程均有根，不满足要求，
当m≠0时，若二次方程x2+2x+m=0有实根，-mx2+2x+1=0无实根，
则
4-4m≥0
4+4m＜0
，
解得m＜-1，
即m∈（-∞，-1）．
故答案为：（-∞，-1）．
点评：本题考查的知识点是二次函数的性质，二次方程根的个数与系数的关系，注意要对m=0进行讨论，尽管对最终答案没有影响．
练习册系列答案
相关题目
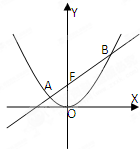抛物线C：x2=2py（p＞0）的焦点为F，O为坐标原点；当抛物线上点N的纵坐标为1时，|NF|=2，已知直线l经过抛物线C的焦点F，且与抛物线C交于A，B两点
（1）求抛物线C的方程；
（2）若△AOB的面积为4，求直线l的方程．
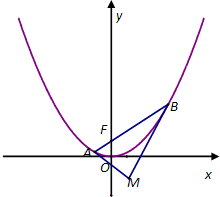如图示：已知抛物线C：x2=4y的焦点为F，过点F作直线l交抛物线C于A、B两点，经过A、B两点分别作抛物线C的切线l1、l2，切线l1与l2相交于点M．
（1）当点A在第二象限，且到准线距离为
5
4
时，求|AB|；
（2）证明：AB⊥MF．
已知α为第三象限角，sinα=-
3
5
，则sin2α+cos2α=
 
．
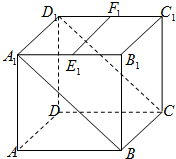如图，A1B1C1D-ABCD为边长为a的正方体，E，F分别是A1B1，C1D的中点，过EF作正方体截面，若截面平行于平面A1BCD1，则截面的面积为
 
．
（文）已知函数f（x）=||x-1|-1|，若关于x的方程f（x）=t（t∈R）恰有四个互不相等的实数根x1、x2、x3、x4（x1＜x2＜x3＜x4），则x1+x2+x3•x4的取值范围是
 
．
抛物线y=-
1
2
（x+2）2-4的开口向
 
，顶点坐标
 
，对称轴
 
，x
 
时，y随x的增大而增大，x
 
时，y随x的增大而减小．
已知平面直角坐标系内的两个向量
a
=（1，2），
b
=（m，3m-2），且平面内的任一向量
c
都可以唯一表示成
c
=λ
a
-μ
b
（λ，μ为实数），则m的取值范围是
 
．
已知复数z1=2+i，z2=a-i，z1•z2是实数，则实数a=（　　）
A、2B、3C、4D、5

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网