题目内容
已知向量
=(1,3),
=(-2,m),“则m=
”是“
⊥
”的( )
| a |
| b |
| 2 |
| 3 |
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:平面向量及应用
分析:根据向量垂直的坐标关系以及充分条件和必要条件的定义即可得到结论.
解答:
解:若
⊥
,则
•
=0,即-2+3m=0,解得m=
,
则m=
是
⊥
的充分必要条件,
故选:C
| a |
| b |
| a |
| b |
| 2 |
| 3 |
则m=
| 2 |
| 3 |
| a |
| b |
故选:C
点评:本题主要考查充分条件和必要条件的判断,根据向量垂直的坐标关系是解决本题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案
相关题目
已知向量
=(x1,y1),
=(x2,y2),若|
|=2,|
|=3,
•
=-6,并且x2+y2≠0,则
的值是( )
| a |
| b |
| a |
| b |
| a |
| b |
| x1+y1 |
| x2+y2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
下列终边相同的是( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、(2k+1)π,(4k+1)π,k∈Z |
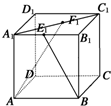 在正方体ABCD-A1B1C1D1中,点E1,F1分别是线段A1B1,A1C1的中点,则直线BE1与AF1所成角的余弦值是( )
在正方体ABCD-A1B1C1D1中,点E1,F1分别是线段A1B1,A1C1的中点,则直线BE1与AF1所成角的余弦值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
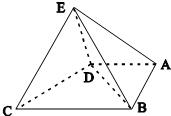 在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.求点A到平面BDE的距离.
在如图所示的几何体中,四边形ABCD是直角梯形,AD∥BC,AB⊥BC,AD=2,AB=3,BC=BE=7,△DCE是边长为6的正三角形.求点A到平面BDE的距离.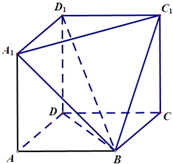 如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.
如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.