题目内容
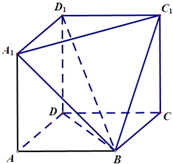 如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.
如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.(1)求证:BD1⊥A1C1.
(2)求该几何体的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)补全四棱柱ABCD-A1B1C1D1,得到四棱柱ABCD-A1B1C1D1是正方体,证出A1C1⊥平面BDD1;即可证出BD1⊥A1C1;
(2)用正方体的体积减去三棱锥的体积,得出几何体的体积.
(2)用正方体的体积减去三棱锥的体积,得出几何体的体积.
解答:
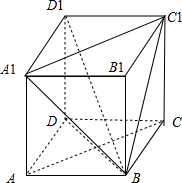 解:(1)证明:连接AC,补全四棱柱ABCD-A1B1C1D1,如图所示;
解:(1)证明:连接AC,补全四棱柱ABCD-A1B1C1D1,如图所示;
∵四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形,
∴四棱柱ABCD-A1B1C1D1是正方体,
∴DD1⊥平面ABCD,
又AC?平面ABCD,∴DD1⊥AC,
∵AC⊥BD,且BD∩DD1=D,∴AC⊥平面BDD1,
又∵AA1∥DD1∥CC1,且AA1=DD1=CC1,
∴四边形ACC1A1是平行四边形,
∴A1C1∥AC,
∴A1C1⊥平面BDD1;
又∵BD1⊥?平面BDD1,
∴BD1⊥A1C1;
(2)该几何体的体积是
V=V正方体ABCD-A1B1C1D1-V三棱锥B-A1B1C1
=13-
•
•12•1
=
.
 解:(1)证明:连接AC,补全四棱柱ABCD-A1B1C1D1,如图所示;
解:(1)证明:连接AC,补全四棱柱ABCD-A1B1C1D1,如图所示;∵四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形,
∴四棱柱ABCD-A1B1C1D1是正方体,
∴DD1⊥平面ABCD,
又AC?平面ABCD,∴DD1⊥AC,
∵AC⊥BD,且BD∩DD1=D,∴AC⊥平面BDD1,
又∵AA1∥DD1∥CC1,且AA1=DD1=CC1,
∴四边形ACC1A1是平行四边形,
∴A1C1∥AC,
∴A1C1⊥平面BDD1;
又∵BD1⊥?平面BDD1,
∴BD1⊥A1C1;
(2)该几何体的体积是
V=V正方体ABCD-A1B1C1D1-V三棱锥B-A1B1C1
=13-
| 1 |
| 3 |
| 1 |
| 2 |
=
| 5 |
| 6 |
点评:本题考查了空间中的垂直于平行的判断与性质的问题,也考查了求空间几何体的体积的问题,解题的关键是补全正方体,是中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
已知向量
=(1,3),
=(-2,m),“则m=
”是“
⊥
”的( )
| a |
| b |
| 2 |
| 3 |
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
若
<
<0,则下列不等式中,正确的不等式有( )
①a+b<ab;②|a|>|b|;③a<b;④ab<b2.
| 1 |
| a |
| 1 |
| b |
①a+b<ab;②|a|>|b|;③a<b;④ab<b2.
| A、1个 | B、2个 | C、3个 | D、4个 |