题目内容
A是锐二面角α-l-β的α内一点,AB⊥β于点B,AB=
,A到l的距离为2,则二面角α-l-β的平面角大小为 .
| 3 |
考点:用空间向量求平面间的夹角
专题:计算题,空间角
分析:由题意画出图形,说明∠AOB是二面角α-l-β的平面角,或补角,然后求出二面角的大小.
解答:
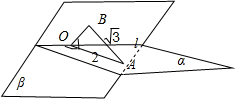 解:由题意可知A是二面角α-l-β的面α内一点,AB⊥平面β于点B,AB=
解:由题意可知A是二面角α-l-β的面α内一点,AB⊥平面β于点B,AB=
,A到l的距离为2,
如图:AO⊥l于O,因为AB⊥平面β于点B,连结OB,所以∠AOB是二面角α-l-β的平面角,或补角,所以sin∠AOB=
,
∴∠AOB=60°或120°.
∵α-l-β是锐二面角,
∴二面角α-l-β的平面角大小为60°.
故答案为:60°
 解:由题意可知A是二面角α-l-β的面α内一点,AB⊥平面β于点B,AB=
解:由题意可知A是二面角α-l-β的面α内一点,AB⊥平面β于点B,AB=| 3 |
如图:AO⊥l于O,因为AB⊥平面β于点B,连结OB,所以∠AOB是二面角α-l-β的平面角,或补角,所以sin∠AOB=
| ||
| 2 |
∴∠AOB=60°或120°.
∵α-l-β是锐二面角,
∴二面角α-l-β的平面角大小为60°.
故答案为:60°
点评:本题考查空间几何体中点、线、面的关系,正确作出所求距离是解题的关键,考查计算能力.

练习册系列答案
相关题目
已知向量
=(1,3),
=(-2,m),“则m=
”是“
⊥
”的( )
| a |
| b |
| 2 |
| 3 |
| a |
| b |
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知Rt△ABC,∠C=90°,CA=3,CB=4,点D、E在AB上,满足
=
,
=-
,则
•
=( )
| AD |
| 1 |
| 3 |
| AB |
| BE |
| 1 |
| 4 |
| AB |
| CE |
| CD |
A、
| ||
B、
| ||
C、
| ||
D、
|