题目内容
已知双曲线的方程为
+
=1,则实数m的取值范围是 .
| x2 |
| m |
| y2 |
| 2m-1 |
考点:双曲线的标准方程
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据方程
+
=1表示双曲线,可知m(2m-1)<0,从而可求实数m的取值范围.
| x2 |
| m |
| y2 |
| 2m-1 |
解答:
解:∵方程
+
=1表示双曲线,
∴m(2m-1)<0
∴0<m<
,
故答案为:0<m<
.
| x2 |
| m |
| y2 |
| 2m-1 |
∴m(2m-1)<0
∴0<m<
| 1 |
| 2 |
故答案为:0<m<
| 1 |
| 2 |
点评:本题考查的重点是双曲线的标准方程,解题的关键是确定双曲线标准方程中平方项的分母异号.

练习册系列答案
相关题目
函数y=(ex-e-x)sinx的图象(部分)大致是( )
A、 |
B、 |
C、 |
D、 |
直线l:y=kx-1与曲线C:x2+y2-4x+3=0有且仅有2个公共点,则实数k的取值范围是( )
A、(0,
| ||||
B、(0,
| ||||
C、{
| ||||
D、{
|
已知函数f(x)=ex,对于曲线y=f(x)上横坐标城等差数列的三个点A、B、C,给出以下四个判断:①△ABC一定是钝角三角形;②△ABC可能是直角三角形;③△ABC可能是等腰三角形;④△ABC不可能是等腰三角形.其中正确的判断是( )
| A、①③ | B、①④ | C、②③ | D、②④ |
(x2+2)(
-1)5的展开式的常数项是( )
| 1 |
| x2 |
| A、2 | B、3 | C、-2 | D、-3 |
 如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,AD⊥CD交⊙O于点E,连接AC、BC、OC、CE,延长AB交CD于F.
如图,已知AB是⊙O的直径,CD是⊙O的切线,C为切点,AD⊥CD交⊙O于点E,连接AC、BC、OC、CE,延长AB交CD于F.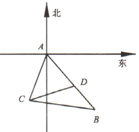 如图,某观测站C在A城的南偏西20°,一条笔直公路AB,其中B在A城南偏东40°,B与C相距31千米.有一人从B出发沿公路向A城走去,走了20千米后到达D处,此时C,D之间的距离为21千米,则A,C之间的距离是
如图,某观测站C在A城的南偏西20°,一条笔直公路AB,其中B在A城南偏东40°,B与C相距31千米.有一人从B出发沿公路向A城走去,走了20千米后到达D处,此时C,D之间的距离为21千米,则A,C之间的距离是