题目内容
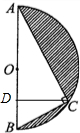
 如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积.(其中∠BAC=30°)
如图所示,半径为R的半圆内的阴影部分以直径AB所在直线为轴,旋转一周得到一几何体,求该几何体的表面积.(其中∠BAC=30°)考点:球内接多面体,球的体积和表面积
专题:计算题,空间位置关系与距离
分析:求出BC=R,AC=
R,CD=
R,再求出几何体的表面积.
| 3 |
| ||
| 2 |
解答:
 解:∵AB为直径,∴∠ACB=90°.
解:∵AB为直径,∴∠ACB=90°.
∵tan∠BAC=
,
∴sin∠BAC=
,
∴BC=R,AC=
R,CD=
R.
∴几何体的表面积为4πR2+
×2π×
R×(R+
R)=
πR2.
 解:∵AB为直径,∴∠ACB=90°.
解:∵AB为直径,∴∠ACB=90°.∵tan∠BAC=
| ||
| 3 |
∴sin∠BAC=
| 1 |
| 2 |
∴BC=R,AC=
| 3 |
| ||
| 2 |
∴几何体的表面积为4πR2+
| 1 |
| 2 |
| ||
| 2 |
| 3 |
11+
| ||
| 2 |
点评:本题考查组合体的表面积的求法,能够熟练运用锐角三角函数的概念进行求解,熟悉圆锥和球的表面积公式是解题的关键.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
在△ABC中,∠A,∠B∠C所对的边为a,b,c,a=7,b=8,cosC=
,则边c2是( )
| 13 |
| 14 |
| A、6 | B、7 | C、8 | D、9 |
已知cos(
-α)=
,则cos(
π+α)=( )
| π |
| 6 |
| 1 |
| 3 |
| 5 |
| 6 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|