题目内容
用数学归纳法证明:1+
+
+…+
<2-
(n∈N*),第二步证明“从k到k+1”,左端增加的项数是( )
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (2n)2 |
| 1 |
| 2n |
| A、1 | B、2 | C、2k | D、8k+4 |
考点:数学归纳法
专题:证明题,点列、递归数列与数学归纳法
分析:当n=k时,写出左端,并当n=k+1时,写出左端,两者比较,关键是最后一项和增加的第一项的关系.
解答:
解:当n=k时,左端=1+
+
+…+
,
那么当n=k+1时 左端=1+
+
+…+
+
,
∴第二步证明“从k到k+1”,左端增加的项数是2.
故选B.
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (2k)2 |
那么当n=k+1时 左端=1+
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| (2k)2 |
| 1 |
| (2k+1)2 |
| 1 |
| (2k+2)2 |
∴第二步证明“从k到k+1”,左端增加的项数是2.
故选B.
点评:此题考查数学归纳法证明,其中关键一步就是从k到k+1,是学习中的难点,也是学习中重点,解答过程中关键是注意最后一项与增添的第一项.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
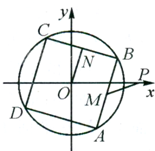 如图,已知点P(
如图,已知点P(| 2 |
| PM |
| ON |
| A、[-2,2] | ||||||||
B、[-
| ||||||||
| C、[-1,1] | ||||||||
D、[-
|
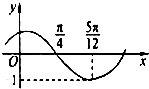 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<| π |
| 2 |
A、右平移
| ||
B、左平移
| ||
C、右平移
| ||
D、左平移
|
已知等差数列{an}中,前19项和为95,则a10等于( )
| A、19 | B、10 | C、9 | D、5 |
按如图程序框图,若输出结果为S=42,则判断框内应补充的条件为( )


| A、i>3 | B、i>5 |
| C、i>7 | D、i>9 |
已知0<α<
<β<π,tan
=
,cos(α-β)=
,则β的值为( )
| π |
| 2 |
| α |
| 2 |
| 1 |
| 2 |
| ||
| 10 |
A、
| ||
B、
| ||
C、
| ||
D、
|