题目内容
直线l1:ax-y+2a+1=0和l2:2x-(a-1)y+2=0,若l1⊥l2,则a= .
考点:直线的一般式方程与直线的垂直关系
专题:直线与圆
分析:由直线的垂直关系可得a的方程,解方程可得.
解答:
解:∵直线l1:ax-y+2a+1=0和l2:2x-(a-1)y+2=0,且l1⊥l2,
∴2a+(-1)[-(a-1)]=0,解得a=
故答案为:
∴2a+(-1)[-(a-1)]=0,解得a=
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查直线的一般式方程和垂直关系,属基础题.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
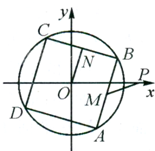 如图,已知点P(
如图,已知点P(| 2 |
| PM |
| ON |
| A、[-2,2] | ||||||||
B、[-
| ||||||||
| C、[-1,1] | ||||||||
D、[-
|
已知直线l1:(1-a)x+ay-2=0,l2:ax+(2a+1)y+3=0,若l1⊥l2,则a的值为( )
| A、0 | B、-2 |
| C、-2或0 | D、0或2 |