题目内容
如果不等式|x-a|＜1成立的充分不必要条件是1＜x＜2，则实数a的取值范围是（ ）
| A、1＜a＜2 |
| B、1≤a≤2 |
| C、a＞2或a＜1 |
| D、a≥2或a≤1 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据不等式的性质，以及充分条件和必要条件的定义即可得到结论．
解答：
解：由|x-a|＜1得a-1＜x＜a+1，
∵1＜x＜2是不等式|x-a|＜1成立的充分不必要条件，
∴满足
，且等号不能同时取得，
即
，
解得1≤a≤2，
故选：B
∵1＜x＜2是不等式|x-a|＜1成立的充分不必要条件，
∴满足
|
即
|
解得1≤a≤2，
故选：B
点评：本题主要考查充分条件和必要条件的应用，根据不等式之间的关系是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
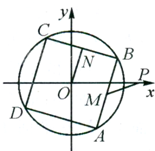如图，已知点P(| 2 |
| PM |
| ON |
| A、[-2，2] | ||||||||
B、[-
| ||||||||
| C、[-1，1] | ||||||||
D、[-
|
已知等差数列{an}中，前19项和为95，则a10等于（ ）
| A、19 | B、10 | C、9 | D、5 |
椭圆
+
=1与双曲线
-
=1有相同的焦点，则实数a的值是（ ）
| x2 |
| 6 |
| y2 |
| a2 |
| x2 |
| a |
| y2 |
| 4 |
A、
| ||
| B、1或-2 | ||
C、1或
| ||
| D、1 |
按如图程序框图，若输出结果为S=42，则判断框内应补充的条件为（ ）
| A、i＞3 | B、i＞5 |
| C、i＞7 | D、i＞9 |
已知直线l1：（1-a）x+ay-2=0，l2：ax+（2a+1）y+3=0，若l1⊥l2，则a的值为（ ）
| A、0 | B、-2 |
| C、-2或0 | D、0或2 |
在三棱柱ABC-A1B1C1中，D是CC1的中点，F是A1B的中点，且
=α
+β
，则（ ）
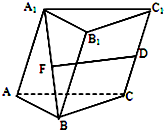
| DF |
| AB |
| AC |
A、α=
| ||
B、α=-
| ||
C、α=1，β=-
| ||
D、α=-1，β=
|
下列函数中，是奇函数的是（ ）
| A、y=2x |
| B、y=-3x2+1 |
| C、y=x3-x |
| D、y=3x2+1 |