题目内容
对于平面几何中的命题“如果两个角的两边分别对应垂直，那么这两个角相等或互补”，在立体几何中，类比上述命题，可以得到命题：“ ”．
考点：类比推理
专题：规律型,推理和证明
分析：本题考查的知识点是类比推理，由平面图形中点的性质类比推理出空间里的线的性质，由平面图形中线的性质类比推理出空间中面的性质，由平面图形中面的性质类比推理出空间中体的性质．故由平面几何中的命题：“如果两个角的两边分别对应垂直，那么这两个角相等或互补”（边角的性质），我们可以推断在立体几何中，相关二面角和形成二面角的两个半平面的性质．
解答：
解：在由平面图形的性质向空间物体的性质进行类比时，
我们常用由平面图形中线的性质类比推理出空间中面的性质，
故由平面几何中的命题：“如果两个角的两边分别对应垂直，那么这两个角相等或互补”（边角的性质），
我们可以推断在立体几何中：
“如果两个二面角的半平面分别对应垂直，那么这两个二面角角相等或互补”（面与二面角的性质），
故答案为：“如果两个二面角的半平面分别对应垂直，那么这两个二面角角相等或互补”．
我们常用由平面图形中线的性质类比推理出空间中面的性质，
故由平面几何中的命题：“如果两个角的两边分别对应垂直，那么这两个角相等或互补”（边角的性质），
我们可以推断在立体几何中：
“如果两个二面角的半平面分别对应垂直，那么这两个二面角角相等或互补”（面与二面角的性质），
故答案为：“如果两个二面角的半平面分别对应垂直，那么这两个二面角角相等或互补”．
点评：类比推理的一般步骤是：（1）找出两类事物之间的相似性或一致性；（2）用一类事物的性质去推测另一类事物的性质，得出一个明确的命题（猜想）．
练习册系列答案
相关题目
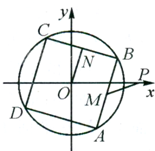如图，已知点P(| 2 |
| PM |
| ON |
| A、[-2，2] | ||||||||
B、[-
| ||||||||
| C、[-1，1] | ||||||||
D、[-
|
已知曲线C：y=
（-2≤x≤0）与函数f（x）=loga（-x）及函数g（x）=a-x（其中a＞1）的图象分别交于A（x1，y1），B（x2，y2），则x12+x22的值为（ ）
| 4-x2 |
| A、16 | B、8 | C、4 | D、2 |
椭圆
+
=1与双曲线
-
=1有相同的焦点，则实数a的值是（ ）
| x2 |
| 6 |
| y2 |
| a2 |
| x2 |
| a |
| y2 |
| 4 |
A、
| ||
| B、1或-2 | ||
C、1或
| ||
| D、1 |
在独立性检验中，统计量x2有两个临界值：3.841和6.635；当x2＞3.841时，有95%的把握说明两个事件有关，当x2＞6.635时，有99%的把握说明两个事件相关，当x2≤3.841时，认为两个事件无关．在一项调查某种药是否对心脏病有治疗作用时，共调查了3000人，经计算的x2=4.56，根据这一数据分析，认为此药物与心脏病之间（ ）
| A、有95%的把握认为两者相关 |
| B、约有95%的心脏病患者使用药物有作用 |
| C、有99%的把握认为两者相关 |
| D、约有99%的心脏病患者使用药物有作用 |