题目内容
平面直角坐标系中,方程|x-1|+|y-1|=1的曲线围成的封闭图形绕y轴旋转一周所形成的几何体的体积为 .
考点:旋转体(圆柱、圆锥、圆台),棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:方程|x-1|+|y-1|=1的曲线围成的封闭图形是一个以(0,1),(1,0),(1,2),(2,1)为顶点的正方形,绕y轴旋转一周所形成的几何体是两个圆台挖去两个圆锥形成的组合体,代入圆台和圆锥体积公式,可得答案.
解答:
解:方程|x-1|+|y-1|=1围成的封闭图形是一个以(0,1),(1,0),(1,2),(2,1)为顶点的正方形,
绕y轴旋转一周所形成的几何体是两个圆台挖去两个圆锥形成的组合体,
如下图所示:

圆台的上底面半径为1,下底面半径为2,高为1,
圆锥的底面半径为1,高为1,
故几何体的体积为:2×[
×π×(1+4+2)-
×π×1]=4π,
故答案为:4π.
绕y轴旋转一周所形成的几何体是两个圆台挖去两个圆锥形成的组合体,
如下图所示:

圆台的上底面半径为1,下底面半径为2,高为1,
圆锥的底面半径为1,高为1,
故几何体的体积为:2×[
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:4π.
点评:本题考查的知识点是旋转体,圆台和圆锥的体积,分析出几何体的形状是解答的关键,难度中档.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
在正方体ABCD-A1B1C1D1中,下列各 式运算结果为向量
的是( )
①(
-
)-
;
②(
+
)-
;
③(
-
)-
;
④(
-
)+
.
| BD1 |
①(
| A1D1 |
| A1A |
| AB |
②(
| BC |
| BB1 |
| D1C1 |
③(
| AD |
| AB |
| DD1 |
④(
| B1D1 |
| A1A |
| DD1 |
| A、①② | B、②③ | C、③④ | D、①④ |
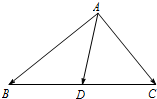 如图,点D是线段BC的中点,BC=6,且|
如图,点D是线段BC的中点,BC=6,且|| AB |
| AC |
| AB |
| AC |
| AD |
| A、6 | ||
B、2
| ||
| C、3 | ||
D、
|
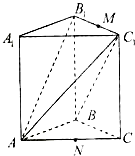 如图,直三棱柱ABC-A1B1C1中,已知∠ABC=90°,AB=BC=4,BB1=3,M、N分别是B1C1和AC的中点.
如图,直三棱柱ABC-A1B1C1中,已知∠ABC=90°,AB=BC=4,BB1=3,M、N分别是B1C1和AC的中点. 已知函数f(x)=
已知函数f(x)=