题目内容
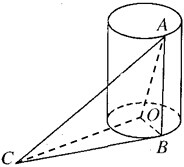 如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线.
如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线.(1)求证:OB⊥AC;
(2)若AC与圆柱下底面所成的角为30°,OA=2.求三棱锥A-BOC的体积.
考点:直线与平面垂直的性质,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)连结OB,根据切线性质有OB⊥BC,根据圆柱的几何特征,可得AB⊥OB,进而由线面垂直的判定定理可得OB⊥平面ABC,进而OB⊥AC;
(2)在Rt△OAB中,OA=2,OB=1,可得AB=
,结合AC与圆柱下底面所成的角即∠ACB=30°,可求出BC,AC,代入棱锥体积公式,可得三棱锥A-BOC的体积.
(2)在Rt△OAB中,OA=2,OB=1,可得AB=
| 3 |
解答:
解:(1)连结OB,
∵BC是下底面的一条切线,
圆的切线性质有OB⊥BC,
又∵AB是圆柱的一条母线,
∴AB⊥底面⊙O,
又OB?底面⊙O,
∴AB⊥OB,
又∵AB∩BC=B,AB,BC?平面ABC,
∴OB⊥平面ABC,
又∵AC?平面ABC,
∴OB⊥AC.
(2)在Rt△OAB中,OA=2,OB=1,
∴AB=
.
又∵AB⊥底面⊙O,
∴∠ACB就是AC与底面⊙O所成角,
∵∠ACB=30°,
∴BC=3,AC=2
,
∴VA-BOC=
AB×S△BOC=
AB×OB×BC=
.
∵BC是下底面的一条切线,
圆的切线性质有OB⊥BC,
又∵AB是圆柱的一条母线,
∴AB⊥底面⊙O,
又OB?底面⊙O,
∴AB⊥OB,
又∵AB∩BC=B,AB,BC?平面ABC,
∴OB⊥平面ABC,
又∵AC?平面ABC,
∴OB⊥AC.
(2)在Rt△OAB中,OA=2,OB=1,
∴AB=
| 3 |
又∵AB⊥底面⊙O,
∴∠ACB就是AC与底面⊙O所成角,
∵∠ACB=30°,
∴BC=3,AC=2
| 3 |
∴VA-BOC=
| 1 |
| 3 |
| 1 |
| 6 |
| ||
| 2 |
点评:本题考查的知识点是直线与平面垂直的判定与性质,圆柱的几何特征,棱锥的体积公式,是空间线面关系的综合应用,难度中档.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 如图:四边形ABCD是梯形,AB∥CD,AD⊥CD,三角形ADE是等边三角形,且平面ABCD⊥平面ADE,EF∥AB,CD=2AB=2AD=2EF=4,
如图:四边形ABCD是梯形,AB∥CD,AD⊥CD,三角形ADE是等边三角形,且平面ABCD⊥平面ADE,EF∥AB,CD=2AB=2AD=2EF=4, 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,AC=1,BC=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,AC=1,BC= 如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥CB,M,N分别是线段AE,AP上的动点,且满足:
如图,平面PAC⊥平面ABC,AC⊥BC,△PAC为等边三角形,PE∥CB,M,N分别是线段AE,AP上的动点,且满足: