题目内容
(1)已知二项式(x2+
)n(n∈N*)展开式中,前三项的二项式系数和为56,求展开式中的常数项;
(2)(1-2x)2014=a0+a1x+a2x2+…+a2014x2014(x∈R)
①求
+
+
+…+
的值;
②求a1+2a2+3a3+4a4+…+2014a2014的值.
| 1 | ||
2
|
(2)(1-2x)2014=a0+a1x+a2x2+…+a2014x2014(x∈R)
①求
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2014 |
| 22014 |
②求a1+2a2+3a3+4a4+…+2014a2014的值.
考点:二项式系数的性质
专题:二项式定理
分析:(1)由题意可得
+
+
=56,求得n的值,在二项式的展开式的通项公式中,令x的幂指数等于0,求得r的值,即可求得展开式中的常数项的值.
(2)①在所给的等式中,令x=0可得a0=1.再令x=
,可得a0+
+
+
+…+
的值,从而求得
+
+
+…+
的值.
②把所给的等式两边同时对x求导数,再令x=1可得a1+2a2+3a3+4a4+…+2014a2014的值.
| C | 0 n |
| C | 1 n |
| C | 2 n |
(2)①在所给的等式中,令x=0可得a0=1.再令x=
| 1 |
| 2 |
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2014 |
| 22014 |
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2014 |
| 22014 |
②把所给的等式两边同时对x求导数,再令x=1可得a1+2a2+3a3+4a4+…+2014a2014的值.
解答:
(1)解:由题意可得
+
+
=1+n+
=56,求得 n=10,
故二项式(x2+
)10展开式的通项公式为 Tr+1=
•2-r•x20-
,
令20-
=0,求得 r=8,故展开式中的常数项为
•2-8=
.
(2)解:①∵(1-2x)2014=a0+a1x+a2x2+…+a2014x2014(x∈R),令x=0可得a0=1.
∴令x=
,可得 a0+
+
+
+…+
=0,故有
+
+
+…+
=-1.
②由(1-2x)2014=a0+a1x+a2x2+…+a2014x2014(x∈R),
可得2014•(-2)•(1-2x)2013 =a1+2a2x+…+2014a2014x2013(x∈R),
再令x=1可得 a1+2a2+3a3+4a4+…+2014a2014=4028.
| C | 0 n |
| C | 1 n |
| C | 2 n |
| n(n-1) |
| 2 |
故二项式(x2+
| 1 | ||
2
|
| C | r 10 |
| 5r |
| 2 |
令20-
| 5r |
| 2 |
| C | 8 10 |
| 45 |
| 256 |
(2)解:①∵(1-2x)2014=a0+a1x+a2x2+…+a2014x2014(x∈R),令x=0可得a0=1.
∴令x=
| 1 |
| 2 |
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2014 |
| 22014 |
| a1 |
| 2 |
| a2 |
| 22 |
| a3 |
| 23 |
| a2014 |
| 22014 |
②由(1-2x)2014=a0+a1x+a2x2+…+a2014x2014(x∈R),
可得2014•(-2)•(1-2x)2013 =a1+2a2x+…+2014a2014x2013(x∈R),
再令x=1可得 a1+2a2+3a3+4a4+…+2014a2014=4028.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,给变量赋值的问题,属于基础题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
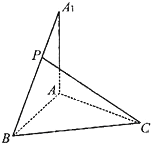 已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点.
已知AA1⊥平面ABC,AA1=AB=BC=CA=3,P为A1B上的点.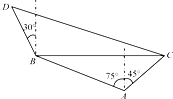 在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离(
在海岸A处,发现北偏西75°的方向,与A距离2海里的B处有一艘走私船,在A处北偏东45°方向,与A距离( 某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小三角形构成,小三角形数越多刺绣越漂亮,现按同样的规律刺绣(小三角形的摆放规律相同),设第n个图形包含f(n)个小三角形.由图形知f(1)=1,f(2)=3,f(3)=6
某少数民族的刺绣有着悠久的历史,如图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都由小三角形构成,小三角形数越多刺绣越漂亮,现按同样的规律刺绣(小三角形的摆放规律相同),设第n个图形包含f(n)个小三角形.由图形知f(1)=1,f(2)=3,f(3)=6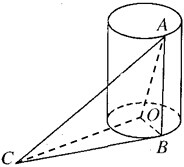 如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线.
如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线.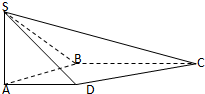 如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=1,
如图,在四棱锥S-ABCD中,SA⊥平面ABCD,底面ABCD为直角梯形,AD∥BC,∠ABC=90°,SA=AB=1,