题目内容
设函数f(x)=(x-2)2ex.
(Ⅰ)求函数f(x)的极值;
(Ⅱ)是否存在[a,b](a<b),使得f(x)在该区间上的值域为[e4a,e4b]?若存在,求出a,b的值;若不存在,说明理由.
(Ⅰ)求函数f(x)的极值;
(Ⅱ)是否存在[a,b](a<b),使得f(x)在该区间上的值域为[e4a,e4b]?若存在,求出a,b的值;若不存在,说明理由.
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由f'(x)=x(x-2)ex,当f′(x)>0时,解得:x>2,x<0,当f(x)<0时,解得:0<x<2,得到函数的单调区间,从而求出函数的极值.
(Ⅱ)分别讨论a=0,a>0的情况,列出方程组,找到单调区间,从而确定出a,b的值.
(Ⅱ)分别讨论a=0,a>0的情况,列出方程组,找到单调区间,从而确定出a,b的值.
解答:
解:(Ⅰ)∵f'(x)=x(x-2)ex,
当f′(x)>0时,解得:x>2,x<0,
当f(x)<0时,解得:0<x<2,
∴f(x)在(-∞,0),(2,+∞)上单调递增,(0,2)上单调递减.
∴y极大=f(0)=4,y极小=f(2)=0;
(Ⅱ)∵f(x)≥0,∴a≥0;
若a=0则b≥2,故有(b-2)2eb=e4b
构造g(b)=
eb(b>2),
∴g′(b)=[
+
]eb>0
b=4为唯一解.
若a>0,则2∉[a,b]即b>a>2或0<a<b<2
①b>a>2时,
前面已证至多一解,
不存在满足条件的a,b;
②0<a<b<2时,
,相除得a(a-2)2ea=b(b-2)2eb
记 h(x)=x(x-2)2ex(0<x<2),
则 h'(x)=(x3-x2-4x+4)ex=(x2-4)(x-1)ex,
∴h(x)在(0,1)递增,(1,2)递减,
由h(a)=h(b),
∴0<a<1,1<b<2
此时(a-2)2ea<4e<e4b矛盾.
综上所述,满足条件的a,b为a=0,b=4.
当f′(x)>0时,解得:x>2,x<0,
当f(x)<0时,解得:0<x<2,
∴f(x)在(-∞,0),(2,+∞)上单调递增,(0,2)上单调递减.
∴y极大=f(0)=4,y极小=f(2)=0;
(Ⅱ)∵f(x)≥0,∴a≥0;
若a=0则b≥2,故有(b-2)2eb=e4b
构造g(b)=
| (b-2)2 |
| b |
∴g′(b)=[
| b2-4 |
| b2 |
| (b-2)2 |
| b |
b=4为唯一解.
若a>0,则2∉[a,b]即b>a>2或0<a<b<2
①b>a>2时,
|
不存在满足条件的a,b;
②0<a<b<2时,
|
记 h(x)=x(x-2)2ex(0<x<2),
则 h'(x)=(x3-x2-4x+4)ex=(x2-4)(x-1)ex,
∴h(x)在(0,1)递增,(1,2)递减,
由h(a)=h(b),
∴0<a<1,1<b<2
此时(a-2)2ea<4e<e4b矛盾.
综上所述,满足条件的a,b为a=0,b=4.
点评:本题考察了函数的单调性,求函数的最值问题,导数的应用,渗透了分类讨论思想,是一道综合题.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
下列命题,正确的是( )
| A、a,b,c∈R,且a>b,则ac>bc | ||||
B、a,b∈R,且ab≠0,则
| ||||
| C、复数Z=i-1对应的点在第四象限 | ||||
| D、a,b∈R,且|a|>|b|,则a2>b2 |
设a>0,b>0,则“a2+b2≤1”是“a+b≤ab+1”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
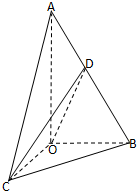 如图,在三棱锥A-BOC中,∠OAB=30°,AO⊥平面BOC,AB=4,∠BOC=90°,BO=CO,D是AB的中点.
如图,在三棱锥A-BOC中,∠OAB=30°,AO⊥平面BOC,AB=4,∠BOC=90°,BO=CO,D是AB的中点.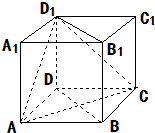 如图,在正方体ABCD-A1B1C1D1中.求证:平面ACD1⊥平面BB1D1D.
如图,在正方体ABCD-A1B1C1D1中.求证:平面ACD1⊥平面BB1D1D.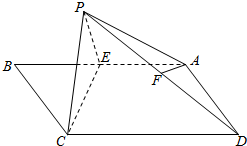 如图,在矩形ABCD中,AB=2,BC=1,E为AB的中点,以直线CE为折线将点B折起至点P,并保持∠PEB为锐角,连接PA,PC,PD,取PD的中点F.
如图,在矩形ABCD中,AB=2,BC=1,E为AB的中点,以直线CE为折线将点B折起至点P,并保持∠PEB为锐角,连接PA,PC,PD,取PD的中点F.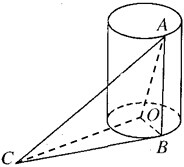 如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线.
如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线.