题目内容
设{an}为等差数列,Sn为数列{an}的前n项和,已知S7=7,S15=75,Tn为数列{|an|}的前n项和,求Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:利用已知条件结合等差数列的前n项和公式,列方程组可求d,a1,代入等差数列的通项公式求an,根据an,的正负情况分n≤3,n>3两种情况进行讨论,利用等差数列的前n项和、添补项求得Tn.
解答:
解:设数列{an}的公差和首项分别为d、a1,
则
,解得a1=-2,d=1,
∴an=-2+(n-1)=n-3,
当n≤3时,Tn=|a1|+|a2|+…+|an|=a1+a2+…+an
=Sn=
=
;
当n>3时,Tn=|a1|+|a2|+…+|an|
=a1+a2+a3-(a4+a5+…+an)
=2(a1+a2+a3)-(a1+a2+a3+a4+a5+…+an)
=2S3-Sn=
,
综上得,Tn=
.
则
|
∴an=-2+(n-1)=n-3,
当n≤3时,Tn=|a1|+|a2|+…+|an|=a1+a2+…+an
=Sn=
| n(a1+an) |
| 2 |
| n(n-5) |
| 2 |
当n>3时,Tn=|a1|+|a2|+…+|an|
=a1+a2+a3-(a4+a5+…+an)
=2(a1+a2+a3)-(a1+a2+a3+a4+a5+…+an)
=2S3-Sn=
| -n2+5n-12 |
| 2 |
综上得,Tn=
|
点评:本题考查了等差数列的通项公式和前n项和公式,考查分类讨论思想和学生的运算求解能力,属中档题.

练习册系列答案
相关题目
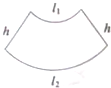 如图是一个扇环(圆环的一部分),两段圆弧的长分别为l1,l2,另外两边的长为h,先把这个扇环与梯形类比,然后根据梯形的面积公式写出这个扇环的面积并证明其正确性.参考公式:
如图是一个扇环(圆环的一部分),两段圆弧的长分别为l1,l2,另外两边的长为h,先把这个扇环与梯形类比,然后根据梯形的面积公式写出这个扇环的面积并证明其正确性.参考公式: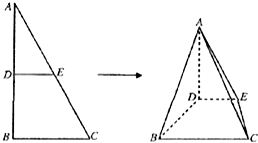 如图,△ABC中,AB=2,BC=1,∠ABC=90°,D,E分别为AB,AC上的点,DE∥BC,将△ADE沿DE折到△A′DE的位置,使平面A′DE⊥平面BCED.
如图,△ABC中,AB=2,BC=1,∠ABC=90°,D,E分别为AB,AC上的点,DE∥BC,将△ADE沿DE折到△A′DE的位置,使平面A′DE⊥平面BCED. 如图,已知,圆O内接四边形BEGD,AB切圆O于点B,且与四边形BEGD对角线ED延长线交于点A,CD切圆O于点D,且与EG延长线交于点C;延长BD交AC于点Q,若AB=AC.
如图,已知,圆O内接四边形BEGD,AB切圆O于点B,且与四边形BEGD对角线ED延长线交于点A,CD切圆O于点D,且与EG延长线交于点C;延长BD交AC于点Q,若AB=AC.