题目内容
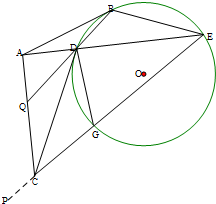
 如图,已知,圆O内接四边形BEGD,AB切圆O于点B,且与四边形BEGD对角线ED延长线交于点A,CD切圆O于点D,且与EG延长线交于点C;延长BD交AC于点Q,若AB=AC.
如图,已知,圆O内接四边形BEGD,AB切圆O于点B,且与四边形BEGD对角线ED延长线交于点A,CD切圆O于点D,且与EG延长线交于点C;延长BD交AC于点Q,若AB=AC.(1)求证:AC∥DG;
(2)求证:C,E,B,Q四点共圆.
考点:与圆有关的比例线段,圆內接多边形的性质与判定
专题:立体几何
分析:(1)若AB=AC,由AB2=AD•AE,得AC2=AD•AE,从而△ADC∽△ACE,由此能证明AC∥DG.
(2)延长EC到P,得∠QCP=∠DGC,由B、E、G、D四点共圆,能证明C、E、B、Q四点共圆.
(2)延长EC到P,得∠QCP=∠DGC,由B、E、G、D四点共圆,能证明C、E、B、Q四点共圆.
解答:
 (本小题满分为10分)
(本小题满分为10分)
证明:(1)若AB=AC,由AB2=AD•AE,得AC2=AD•AE,
即
=
,又∠EAC=∠DAC,
∴△ADC∽△ACE,(3分)
得∠ACD=∠DEG,
又∠CDG=∠DEC=∠DCG,(5分)
∴∠ACD=∠CDG,
故AC∥DG.(6分)
(2)延长EC到P,得∠QCP=∠DGC,
∵B、E、G、D四点共圆,∴∠DGC=∠DBE,
∴∠QCP=∠DGC=∠DBE,
∴C、E、B、Q四点共圆.(10分)
 (本小题满分为10分)
(本小题满分为10分)证明:(1)若AB=AC,由AB2=AD•AE,得AC2=AD•AE,
即
| AC |
| AD |
| AE |
| AC |
∴△ADC∽△ACE,(3分)
得∠ACD=∠DEG,
又∠CDG=∠DEC=∠DCG,(5分)
∴∠ACD=∠CDG,
故AC∥DG.(6分)
(2)延长EC到P,得∠QCP=∠DGC,
∵B、E、G、D四点共圆,∴∠DGC=∠DBE,
∴∠QCP=∠DGC=∠DBE,
∴C、E、B、Q四点共圆.(10分)
点评:本题考查直线平行的证明,考查四点共圆的证明,解题时要认真审题,注意圆的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目