题目内容
从1,2,3,4,5,6六个数字中,选出一个偶数和两个奇数,组成一个没有重复数字的三位数,这样的三位数共有 个.(用数字作答)
考点:计数原理的应用
专题:排列组合
分析:根据先选再排的原则,从1,2,3,4,5,6六个数字中,选出一个偶数和两个奇数有
•
,再进行全排列,问题得以解决.
| C | 1 3 |
| C | 2 3 |
解答:
解:由题意,选出一个偶数和两个奇数有
•
=9种,
再进行全排列,这样的三位数共有
•
=54.
故答案为:54.
| C | 1 3 |
| C | 2 3 |
再进行全排列,这样的三位数共有
| C | 1 3 |
| C | 2 3 |
| •A | 3 3 |
故答案为:54.
点评:本题考查排列、组合及简单计数问题,解题的关键是正确理解偶的含义,以及计数原理,且能根据问题的要求进行分类讨论,本题考查了推理判断的能力及运算能力

练习册系列答案
相关题目
M(a,b)为圆x2+y2=r2(r>0)内异于圆心的一点,则直线ax+by=r2与该圆的位置关系是( )
| A、相切 | B、相交 |
| C、相离 | D、相切或相交 |
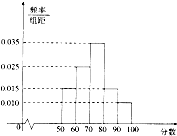 某中学组织全校340名学生参加消防知识竞赛,成绩如图所示,其中得分在区间[90,100]内的人数为
某中学组织全校340名学生参加消防知识竞赛,成绩如图所示,其中得分在区间[90,100]内的人数为