题目内容
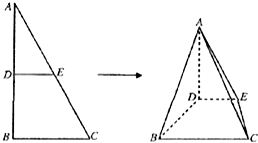 如图,△ABC中,AB=2,BC=1,∠ABC=90°,D,E分别为AB,AC上的点,DE∥BC,将△ADE沿DE折到△A′DE的位置,使平面A′DE⊥平面BCED.
如图,△ABC中,AB=2,BC=1,∠ABC=90°,D,E分别为AB,AC上的点,DE∥BC,将△ADE沿DE折到△A′DE的位置,使平面A′DE⊥平面BCED.(1)当D为AB的中点时,设平面A′BC与平面A′DE所成的二面角的平面角为α(0<α<
| π |
| 2 |
(2)当D点在AB边上运动时,求四梭锥A′-BCED体积的最大值.
考点:棱柱、棱锥、棱台的体积,直线与平面所成的角
专题:综合题,空间位置关系与距离,空间角
分析:(1)先找出α、β,求出tanβ=
,利用两角和的正切公式,求tan(α+β)的值;
(2)表示出求四梭锥A′-BCED体积,利用导数求最大值.
| ||
| 2 |
(2)表示出求四梭锥A′-BCED体积,利用导数求最大值.
解答:
解:(1)作CF⊥DE于F,连接A′F,则CF⊥平面A′DE,
∴∠CA′F=β,
在矩形BCFD中,CF=BD=1,DF=BC=1,
在Rt△A′DF中,A′F=
,tanβ=
=
,
作A′P∥DE,∵DE∥BC,
∴A′P∥BC,
∵平面A′BC∩平面A′DE=A′P,A′P⊥A′D,A′P⊥A′B,
∴∠BA′D=α=
,
∴tan(α+β)
=3+2
(2)设A′D=x,x∈(0,2),则DE=
,BD=2-x,
∴四梭锥A′-BCED体积V=
•
•x=
,
∴V′=
,
令V′=0,可得x=
,且在(0,
)递增,在(
,2)递减,
∴x=
时,四梭锥A′-BCED体积的最大值为
.
∴∠CA′F=β,
在矩形BCFD中,CF=BD=1,DF=BC=1,
在Rt△A′DF中,A′F=
| 2 |
| CF |
| A′F |
| ||
| 2 |
作A′P∥DE,∵DE∥BC,
∴A′P∥BC,
∵平面A′BC∩平面A′DE=A′P,A′P⊥A′D,A′P⊥A′B,
∴∠BA′D=α=
| π |
| 4 |
∴tan(α+β)
1+
| ||||
1-
|
| 2 |
(2)设A′D=x,x∈(0,2),则DE=
| x |
| 2 |
∴四梭锥A′-BCED体积V=
| 1 |
| 3 |
(
| ||
| 2 |
| 4x-x3 |
| 12 |
∴V′=
| 4-3x2 |
| 12 |
令V′=0,可得x=
2
| ||
| 3 |
2
| ||
| 3 |
2
| ||
| 3 |
∴x=
2
| ||
| 3 |
4
| ||
| 27 |
点评:本题考查空间角,考查体积的计算,考查导数知识的运用,综合性强.

练习册系列答案
相关题目
 如图是一个几何体的三视图,根据图中数据:
如图是一个几何体的三视图,根据图中数据: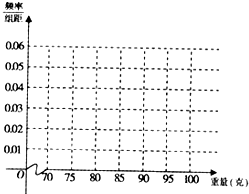 从某批苹果中随机抽取100个苹果进行重量(单位:克)调查.发现重量都在70克至100克之间,结果如表:
从某批苹果中随机抽取100个苹果进行重量(单位:克)调查.发现重量都在70克至100克之间,结果如表: