题目内容
如图,抛物线E: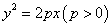 的焦点为
的焦点为 ,其准线
,其准线 与
与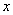 轴交于点
轴交于点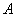 ,过抛物线E上的动点
,过抛物线E上的动点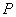 作
作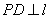 于点
于点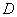 .当
.当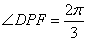 时,
时, 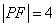 .
.
(Ⅰ)求抛物线E的方程;
(Ⅱ)过点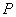 作直线
作直线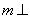
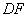 ,求直线
,求直线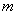 与抛物线E的交点个数;
与抛物线E的交点个数;
(Ⅲ)点C是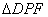 的外心,是否存在点
的外心,是否存在点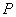 ,使得
,使得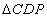 的面积最小.若存在,请求出面积的最小值及P的坐标;若不存在,请说明理由.
的面积最小.若存在,请求出面积的最小值及P的坐标;若不存在,请说明理由.
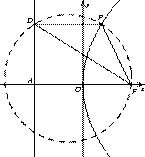
 解:(Ⅰ)过点
解:(Ⅰ)过点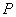 作
作 轴于点
轴于点 ,
, 当
当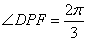 时,
时,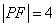 ,
,
 ,
,

 , 1分
, 1分
 中,
中, , 2分
, 2分
 .
. ,即
,即  , 3分
, 3分
 抛物线E的方程:
抛物线E的方程: , 4分
, 4分
(也可由余弦定理求得 ,在
,在 中,
中, ,即
,即 )
)
 (Ⅱ) 解法一:当点
(Ⅱ) 解法一:当点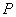 为原点
为原点 时,直线
时,直线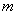 的方程:
的方程: 与抛物线E切于点
与抛物线E切于点 ;
;
设 ,则
,则 ,
, ,
, ,
, , 5分
, 5分
直线 ,化简得:
,化简得: ,
,
代入 得
得 , 6分
, 6分
 ,
, (
( ), 7分
), 7分
 直线
直线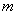 与抛物线E有且只有一个交点
与抛物线E有且只有一个交点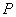 . 8分
. 8分
解法二:由(Ⅰ)得 ,设
,设 ,则
,则 , 5分
, 5分
 ,
, ,直线
,直线 ,即
,即 , 6分
, 6分
代入 中,得
中,得 , 7分
, 7分
 ,
, 直线
直线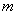 与抛物线E有且只有一个交点
与抛物线E有且只有一个交点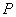 . 8分
. 8分
(Ⅲ)解法一:由已知得DP的中垂线: ,与直线
,与直线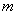 :
: 联立,
联立,
得到圆心C的纵坐标 , 9分
, 9分
 ,
,
又 ,则
,则 , 10分
, 10分
不妨设 (
( ),
),
 , 11分
, 11分
由 得
得 ,由
,由 得
得 ,
,
 当
当 时,函数
时,函数 有最小值;
有最小值;
 当点
当点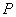 的坐标为
的坐标为 或
或 时, 12分
时, 12分
 取得最小值. 13分
取得最小值. 13分
解法二:由(Ⅱ)得DP的中垂线: ,又直线
,又直线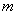 :
: 垂直平分
垂直平分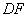 ,
,

 圆心C的纵坐标:
圆心C的纵坐标: , 9分
, 9分
 ,又
,又 ,
,
则 , 10分
, 10分
不妨设 (
( ),
),
 , 11分
, 11分
 在
在 递减,在
递减,在 递增;
递增; 当
当 时,函数
时,函数 有最小值;
有最小值;
 当点
当点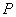 的坐标为
的坐标为 或
或 时, 12分
时, 12分
 取得最小值. 13分
取得最小值. 13分
解法三:设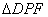 外接的圆C半径为
外接的圆C半径为 ,
, ,不妨设
,不妨设 ,
,
 ,
, , 9分
, 9分
由正弦定理得: ,
,
 ,又
,又 ,
,
 ,则
,则 . 10分
. 10分
以下解法同上.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
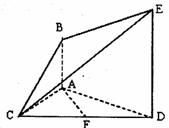
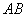 ⊥平面
⊥平面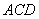 ,
,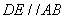 ,
,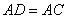
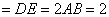 ,且
,且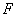 是
是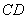 的中点,
的中点,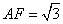 .
.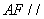 平面
平面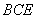 ;
;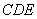 ;
;
 满足: 当
满足: 当 时,
时, ,则
,则 项和
项和




 中,
中, ,
, ,过点D的直线分别交直线AB,AC于点M,N.若
,过点D的直线分别交直线AB,AC于点M,N.若 , 则
, 则 的最小值是 .
的最小值是 .
 ≤
≤ ”的否定是
”的否定是  在点
在点 处的切线方程为
处的切线方程为  ,则
,则 的值为_________
的值为_________ ,则z-|z|对应的点所在的象限为( )
,则z-|z|对应的点所在的象限为( )