题目内容
如图,已知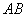 ⊥平面
⊥平面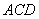 ,
,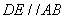 ,
,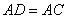
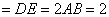 ,且
,且 是
是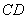 的中点,
的中点,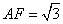 .
.
(1)求证: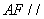 平面
平面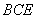 ;
;
(2)求证:平面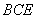 ⊥平面
⊥平面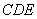 ;
;
(3)求此多面体的体积.
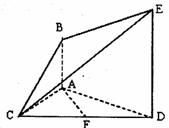
.解:(1)取CE中点P,连结FP、BP,
∵F为CD的中点,
∴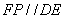 ,且FP=
,且FP=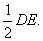
又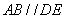 ,且AB=
,且AB=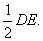
∴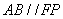 ,且AB=FP,
,且AB=FP,
∴ABPF为平行四边形,∴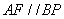 . ……………2分
. ……………2分
又∵AF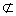 平面BCE,BP
平面BCE,BP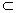 平面BCE,
平面BCE,
∴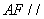 平面BCE ………………………4分
平面BCE ………………………4分
(2)∵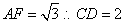 ,所以△ACD为正三角形,∴AF⊥CD
,所以△ACD为正三角形,∴AF⊥CD
∵AB⊥平面ACD,DE//AB
∴DE⊥平面ACD 又AF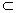 平面ACD
平面ACD
∴DE⊥AF ………………………6分
又AF⊥CD,CD∩DE=D
∴AF⊥平面CDE
又BP∥AF ∴BP⊥平面CDE
又∵BP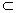 平面BCE
平面BCE
∴平面BCE⊥平面CDE ………………………8分
(3)此多面体是一个以C为顶点,以四边形ABED为底边的四棱锥,
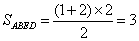 , ………………………10分
, ………………………10分
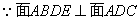 ,
,
 等边三角形AD边上的高就是四棱锥的高
等边三角形AD边上的高就是四棱锥的高
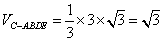 ………………………12分
………………………12分

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 B.
B. C.
C. D.
D.

 ,若直线
,若直线 与圆
与圆 相切,且切点在第二象限,则实数
相切,且切点在第二象限,则实数 .
. 时,则该程序运行后输出的结果是
时,则该程序运行后输出的结果是
 过圆
过圆 的圆心,且与直线
的圆心,且与直线 垂直,则直线
垂直,则直线 满足
满足 ,则
,则 =( )
=( ) B.
B. C.
C. D.
D.
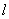 过抛物线
过抛物线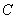 :
: 的焦点,且与
的焦点,且与 轴垂直,则直线
轴垂直,则直线 B.
B. C.
C. D.
D.
 表示的点落在 ( )
表示的点落在 ( )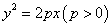 的焦点为
的焦点为 ,其准线
,其准线 与
与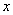 轴交于点
轴交于点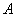 ,过抛物线E上的动点
,过抛物线E上的动点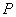 作
作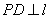 于点
于点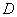 .当
.当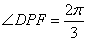 时,
时, 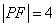 .
.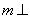
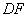 ,求直线
,求直线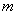 与抛物线E的交点个数;
与抛物线E的交点个数;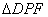 的外心,是否存在点
的外心,是否存在点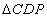 的面积最小.若存在,请求出面积的最小值及P的坐标;若不存在,请说明理由.
的面积最小.若存在,请求出面积的最小值及P的坐标;若不存在,请说明理由.