题目内容
7.某同学从语文、数学、英语、物理、化学、生物六科中选择三个学科参加测试,则数学和物理不同时被选中的概率为$\frac{4}{5}$.分析 先求出数学和物理同时被选中的情况几种,由此能求出数学和物理不同时被选中的概率.
解答 解:某同学从语文、数学、英语、物理、化学、生物六科中选择三个学科参加测试,
基本事件总数n=${C}_{6}^{3}$=20,
数学和物理同时被选中的情况有:${C}_{2}^{2}{C}_{4}^{1}$=4,
∴数学和物理不同时被选中的概率为:
p=1-$\frac{{C}_{2}^{2}{C}_{4}^{1}}{{C}_{6}^{3}}$=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意对立事件概率计算公式的合理运用.

练习册系列答案
相关题目
2.设Sn为等差数列{an}的前n项和,若a1=1,S7=70,则a2=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
12.已知集合A={x|x2-x-2>0},B={x|1<x≤3},则(∁RA)∩B=( )
| A. | A、(1,2] | B. | [-1,2] | C. | (1,3] | D. | (-∞,-1)∪(2,+∞) |
17.函数f(x)=sin(ωx+φ)(ω>0)的一段图象如图所示,则ω=( )
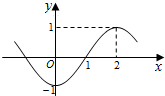
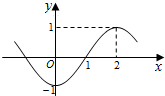
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{2}$ |