题目内容
15．曲线f（x）=x2+lnx在（1，f（1））处的切线的斜率为3．分析 求函数的导数，利用导数的几何意义进行求解即可．
解答 解：函数的导数f′（x）=2x+$\frac{1}{x}$，
则f′（1）=2+1=3，
即f（x）在（1，f（1））处的切线的斜率k=f′（1）=3，
故答案为：3．
点评 本题主要考查导数的几何意义的应用，跟姐姐切线斜率和导数之间的关系是解决本题的关键．比较基础．
练习册系列答案
相关题目
6．下列有关命题的说法错误的是（ ）
| A． | 若“p∨q”为假命题，则p，q均为假命题 | |
| B． | “x=1”是“x≥1”的充分不必要条件 | |
| C． | “sinx=$\frac{1}{2}$”的必要不充分条件是“x=$\frac{π}{6}$” | |
| D． | 若命题p：?x0∈R，x02≥0，则命题￢p：?x∈R，x2＜0 |
3．已知函数f（x）=2sin（ωx+φ）+1（0＜ω＜3，0＜φ＜$\frac{π}{2}$）的一系列对应值如下表：
（1）根据表格提供的数据求函败y=f（x）的解析式；
（2）求函数y=f（x）的单调递增区间与对称中心坐标；
（3）函数y=mf（x）-1在（-$\frac{π}{12}$，$\frac{π}{3}$）上有零点，求实数m的取值范围．
| x | -$\frac{π}{3}$ | -$\frac{π}{12}$ | 0 | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{2π}{3}$ | $\frac{11π}{12}$ |
| f（x） | -1 | 1 | 2 | 3 | 1 | -1 | 1 |
（2）求函数y=f（x）的单调递增区间与对称中心坐标；
（3）函数y=mf（x）-1在（-$\frac{π}{12}$，$\frac{π}{3}$）上有零点，求实数m的取值范围．
10．已知f（x）=$\frac{{2}^{x+1}+1}{{2}^{x}-1}$，且对于任意x∈[1，3]，不等式f（x）＞|x-2|+m恒成立，则m的取值范围是（ ）
| A． | （-∞，-4] | B． | （-$\frac{1}{2}$，+∞） | C． | （-∞，-$\frac{9}{8}$） | D． | （-∞，$\frac{10}{7}$） |
20．若复数z=$\frac{2-i}{i^3}$（i是虚数单位），则z的共轭复数为（ ）
| A． | 1-2i | B． | 1+2i | C． | -1-2i | D． | -1+2i |
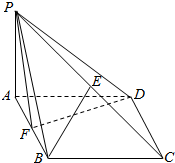如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，∠BAD=45°，AB=2，AD=$\sqrt{2}$，PA⊥平面ABCD，E是PC的中点，F是AB的中点．